More precisely, the full subcategory of the category $\mathcal{M}^{\mathrm{cld}}_{\mathbb {E}_{\infty }}(\mathsf{Sets}_{*})$ of  spanned by the closed symmetric monoidal categories $\left(\phantom{\mathrlap {\lambda ^{\mathsf{Sets}_{*}}}}\mathsf{Sets}_{*}\right.$, $\otimes _{\mathsf{Sets}_{*}}$, $[-_{1},-_{2}]_{\mathsf{Sets}_{*}}$, $\mathbb {1}_{\mathsf{Sets}_{*}}$, $\lambda ^{\mathsf{Sets}_{*}}$, $\rho ^{\mathsf{Sets}_{*}}$, $\left.\sigma ^{\mathsf{Sets}_{*}}\right)$ satisfying Item 1 and Item 2 is contractible (i.e. equivalent to the punctual category).
spanned by the closed symmetric monoidal categories $\left(\phantom{\mathrlap {\lambda ^{\mathsf{Sets}_{*}}}}\mathsf{Sets}_{*}\right.$, $\otimes _{\mathsf{Sets}_{*}}$, $[-_{1},-_{2}]_{\mathsf{Sets}_{*}}$, $\mathbb {1}_{\mathsf{Sets}_{*}}$, $\lambda ^{\mathsf{Sets}_{*}}$, $\rho ^{\mathsf{Sets}_{*}}$, $\left.\sigma ^{\mathsf{Sets}_{*}}\right)$ satisfying Item 1 and Item 2 is contractible (i.e. equivalent to the punctual category).
Unwinding the Statement
Let $(\mathsf{Sets}_{*},\otimes _{\mathsf{Sets}_{*}},[-_{1},-_{2}]_{\mathsf{Sets}_{*}},\mathbb {1}_{\mathsf{Sets}_{*}},\lambda ',\rho ',\sigma ')$ be a closed symmetric monoidal category satisfying Item 1 and Item 2. We need to show that the identity functor
\[ \operatorname {\mathrm{id}}_{\mathsf{Sets}_{*}}\colon \mathsf{Sets}_{*}\to \mathsf{Sets}_{*} \]
admits a unique closed symmetric monoidal functor structure
\[ \begin{array}{cccc} \phantom{\operatorname {\mathrm{id}}^{\otimes }_{\mathsf{Sets}_{*}}}\mathllap {\operatorname {\mathrm{id}}^{\otimes }_{\mathsf{Sets}_{*}}} \colon \mkern -10mu & X\otimes _{\mathsf{Sets}_{*}}Y \mkern -10mu& {}\mathbin {\overset {\scriptstyle \mathord {\sim }}{\dashrightarrow }}& \mkern -10mu{}X\wedge Y,\\ \phantom{\operatorname {\mathrm{id}}^{\otimes }_{\mathsf{Sets}_{*}}}\mathllap {\operatorname {\mathrm{id}}^{\operatorname {\mathrm{Hom}}}_{\mathsf{Sets}_{*}}} \colon \mkern -10mu & [X,Y]_{\mathsf{Sets}_{*}} \mkern -10mu& {}\mathbin {\overset {\scriptstyle \mathord {\sim }}{\dashrightarrow }}& \mkern -10mu{}\mathsf{Sets}_{*}(X,Y),\\ \phantom{\operatorname {\mathrm{id}}^{\otimes }_{\mathsf{Sets}_{*}}}\mathllap {\operatorname {\mathrm{id}}^{\otimes }_{\mathbb {1}|\mathsf{Sets}_{*}}} \colon \mkern -10mu & \mathbb {1}_{\mathsf{Sets}_{*}} \mkern -10mu& {}\mathbin {\overset {\scriptstyle \mathord {\sim }}{\dashrightarrow }}& \mkern -10mu{}S^{0}, \end{array} \]
making it into a symmetric monoidal strongly closed isomorphism of categories from $\left(\phantom{\mathrlap {\lambda '}}\mathsf{Sets}_{*}\right.$, $\otimes _{\mathsf{Sets}_{*}}$, $[-_{1},-_{2}]_{\mathsf{Sets}_{*}}$, $\mathbb {1}_{\mathsf{Sets}_{*}}$, $\lambda '$, $\rho '$, $\left.\sigma '\right)$ to the closed symmetric monoidal category $\left(\phantom{\mathrlap {\lambda ^{\mathsf{Sets}_{*}}}}\mathsf{Sets}_{*}\right.$, $\times $, $\mathsf{Sets}_{*}(-_{1},-_{2})$, $\mathbb {1}_{\mathsf{Sets}_{*}}$, $\lambda ^{\mathsf{Sets}_{*}}$, $\rho ^{\mathsf{Sets}_{*}}$, $\left.\sigma ^{\mathsf{Sets}_{*}}\right)$ of Proposition 7.5.9.1.1.
Constructing an Isomorphism $[-_{1},-_{2}]_{\mathsf{Sets}_{*}}\cong \mathsf{Sets}_{*}(-_{1},-_{2})$
By  , we have a natural isomorphism
, we have a natural isomorphism
\[ \mathsf{Sets}_{*}(S^{0},[-_{1},-_{2}]_{\mathsf{Sets}_{*}})\cong \mathsf{Sets}_{*}(-_{1},-_{2}). \]
By Chapter 6: Pointed Sets, Item 4 of Proposition 6.1.4.1.1, we also have a natural isomorphism
\[ \mathsf{Sets}_{*}(S^{0},[-_{1},-_{2}]_{\mathsf{Sets}_{*}})\cong [-_{1},-_{2}]_{\mathsf{Sets}_{*}}. \]
Composing both natural isomorphisms, we obtain a natural isomorphism
\[ \mathsf{Sets}_{*}(-_{1},-_{2})\cong [-_{1},-_{2}]_{\mathsf{Sets}_{*}}. \]
Given $X,Y\in \operatorname {\mathrm{Obj}}(\mathsf{Sets}_{*})$, we will write
\[ \operatorname {\mathrm{id}}^{\operatorname {\mathrm{Hom}}}_{X,Y}\colon \mathsf{Sets}_{*}(X,Y)\overset {\scriptstyle \mathord {\sim }}{\dashrightarrow }[X,Y]_{\mathsf{Sets}_{*}} \]
for the component of this isomorphism at $(X,Y)$.
Constructing an Isomorphism $\mathord {\otimes _{\mathsf{Sets}_{*}}}\cong \mathord {\wedge }$
Since $\otimes _{\mathsf{Sets}_{*}}$ is adjoint in each variable to $[-_{1},-_{2}]_{\mathsf{Sets}_{*}}$ by assumption and $\wedge $ is adjoint in each variable to $\mathsf{Sets}_{*}(-_{1},-_{2})$ by Chapter 4: Constructions With Sets, Item 2 of Proposition 4.3.5.1.2, uniqueness of adjoints ( ) gives us natural isomorphisms
) gives us natural isomorphisms
\begin{align*} X\otimes _{\mathsf{Sets}_{*}}- & \cong X\wedge -,\\ -\otimes _{\mathsf{Sets}_{*}}Y & \cong Y\wedge -. \end{align*}
By  , we then have $\mathord {\otimes _{\mathsf{Sets}_{*}}}\cong \mathord {\wedge }$. We will write
, we then have $\mathord {\otimes _{\mathsf{Sets}_{*}}}\cong \mathord {\wedge }$. We will write
\[ \operatorname {\mathrm{id}}^{\otimes }_{\mathsf{Sets}_{*}|X,Y}\colon X\otimes _{\mathsf{Sets}_{*}}Y\overset {\scriptstyle \mathord {\sim }}{\dashrightarrow }X\wedge Y \]
for the component of this isomorphism at $(X,Y)$.
Alternative Construction of an Isomorphism $\mathord {\otimes _{\mathsf{Sets}_{*}}}\cong \mathord {\wedge }$
Alternatively, we may construct a natural isomorphism $\mathord {\otimes _{\mathsf{Sets}_{*}}}\cong \mathord {\wedge }$ as follows:
-
1.
Let $X\in \operatorname {\mathrm{Obj}}(\mathsf{Sets}_{*})$.
-
2.
Since $\otimes _{\mathsf{Sets}_{*}}$ is part of a closed monoidal structure, it preserves colimits in each variable by  .
.
-
3.
Since $X\cong \bigvee _{x\in X^{-}}S^{0}$ and $\otimes _{\mathsf{Sets}_{*}}$ preserves colimits in each variable, we have
\begin{align*} X\otimes _{\mathsf{Sets}_{*}}Y & \cong (\bigvee _{x\in X^{-}}S^{0})\otimes _{\mathsf{Sets}_{*}}Y\\ & \cong \bigvee _{x\in X^{-}}(S^{0}\otimes _{\mathsf{Sets}_{*}}Y)\\ & \cong \bigvee _{x\in X^{-}}Y\\ & \cong \bigvee _{x\in X^{-}}S^{0}\wedge Y\\ & \cong (\bigvee _{x\in X^{-}}S^{0})\wedge Y\\ & \cong X\wedge Y, \end{align*}
naturally in $Y\in \operatorname {\mathrm{Obj}}(\mathsf{Sets}_{*})$, where we have used that $S^{0}$ is the monoidal unit for $\otimes _{\mathsf{Sets}_{*}}$. Thus $X\otimes _{\mathsf{Sets}_{*}}-\cong X\wedge -$ for each $X\in \operatorname {\mathrm{Obj}}(\mathsf{Sets}_{*})$.
-
4.
Similarly, $-\otimes _{\mathsf{Sets}_{*}}Y\cong -\wedge Y$ for each $Y\in \operatorname {\mathrm{Obj}}(\mathsf{Sets}_{*})$.
-
5.
By  , we then have $\mathord {\otimes _{\mathsf{Sets}_{*}}}\cong \mathord {\wedge }$.
, we then have $\mathord {\otimes _{\mathsf{Sets}_{*}}}\cong \mathord {\wedge }$.
Below, we’ll show that if a natural isomorphism $\mathord {\otimes _{\mathsf{Sets}_{*}}}\cong \mathord {\wedge }$ exists, then it must be unique. This will show that the isomorphism constructed above is equal to the isomorphism $\operatorname {\mathrm{id}}^{\otimes }_{\mathsf{Sets}_{*}|X,Y}\colon X\otimes _{\mathsf{Sets}_{*}}Y\to X\wedge Y$ from before.
Constructing an Isomorphism $\operatorname {\mathrm{id}}^{\otimes }_{\mathbb {1}}\colon \mathbb {1}_{\mathsf{Sets}_{*}}\to S^{0}$
We define an isomorphism $\operatorname {\mathrm{id}}^{\otimes }_{\mathbb {1}}\colon \mathbb {1}_{\mathsf{Sets}_{*}}\to S^{0}$ as the composition
\[ \mathbb {1}_{\mathsf{Sets}_{*}}\overset {\rho ^{\mathsf{Sets}_{*},-1}_{\mathbb {1}_{\mathsf{Sets}_{*}}}}{\underset {\scriptstyle \mathord {\sim }}{\dashrightarrow }}\mathbb {1}_{\mathsf{Sets}_{*}}\wedge S^{0}\overset {\operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathsf{Sets}_{*}|\mathbb {1}_{\mathsf{Sets}_{*}}}}{\underset {\scriptstyle \mathord {\sim }}{\dashrightarrow }}\mathbb {1}_{\mathsf{Sets}_{*}}\otimes _{\mathsf{Sets}_{*}} S^{0}\overset {\lambda '_{ S^{0}}}{\underset {\scriptstyle \mathord {\sim }}{\dashrightarrow }}S^{0} \]
in $\mathsf{Sets}_{*}$.
Monoidal Left Unity of the Isomorphism $\mathord {\otimes _{\mathsf{Sets}_{*}}}\cong \mathord {\wedge }$
We have to show that the diagram commutes. To this end, we will first show that the diagram corresponding to the case $X=S^{0}$, commutes. Indeed, consider the diagram whose boundary diagram corresponds to the diagram $(\dagger )$ above. In this diagram:
-
•
Subdiagrams $(1)$, $(2)$, and $(3)$ commute by the naturality of $\operatorname {\mathrm{id}}^{\otimes }_{\mathsf{Sets}_{*}}$.
-
•
Subdiagram $(4)$ commutes by  .
.
-
•
Subdiagram $(5)$ commutes by the naturality of $\rho ^{\mathsf{Sets}_{*},-1}$.
-
•
Subdiagram $(6)$ commutes trivially.
-
•
Subdiagram $(7)$ commutes by the naturality of $\rho ^{\mathsf{Sets}_{*}}$, where the equality $\rho ^{\mathsf{Sets}_{*}}_{S^{0}}=\lambda ^{\mathsf{Sets}_{*}}_{S^{0}}$ comes from  .
.
Since all subdiagrams commute, so does the boundary diagram, i.e. the diagram $(\dagger )$ above. As a result, the diagram
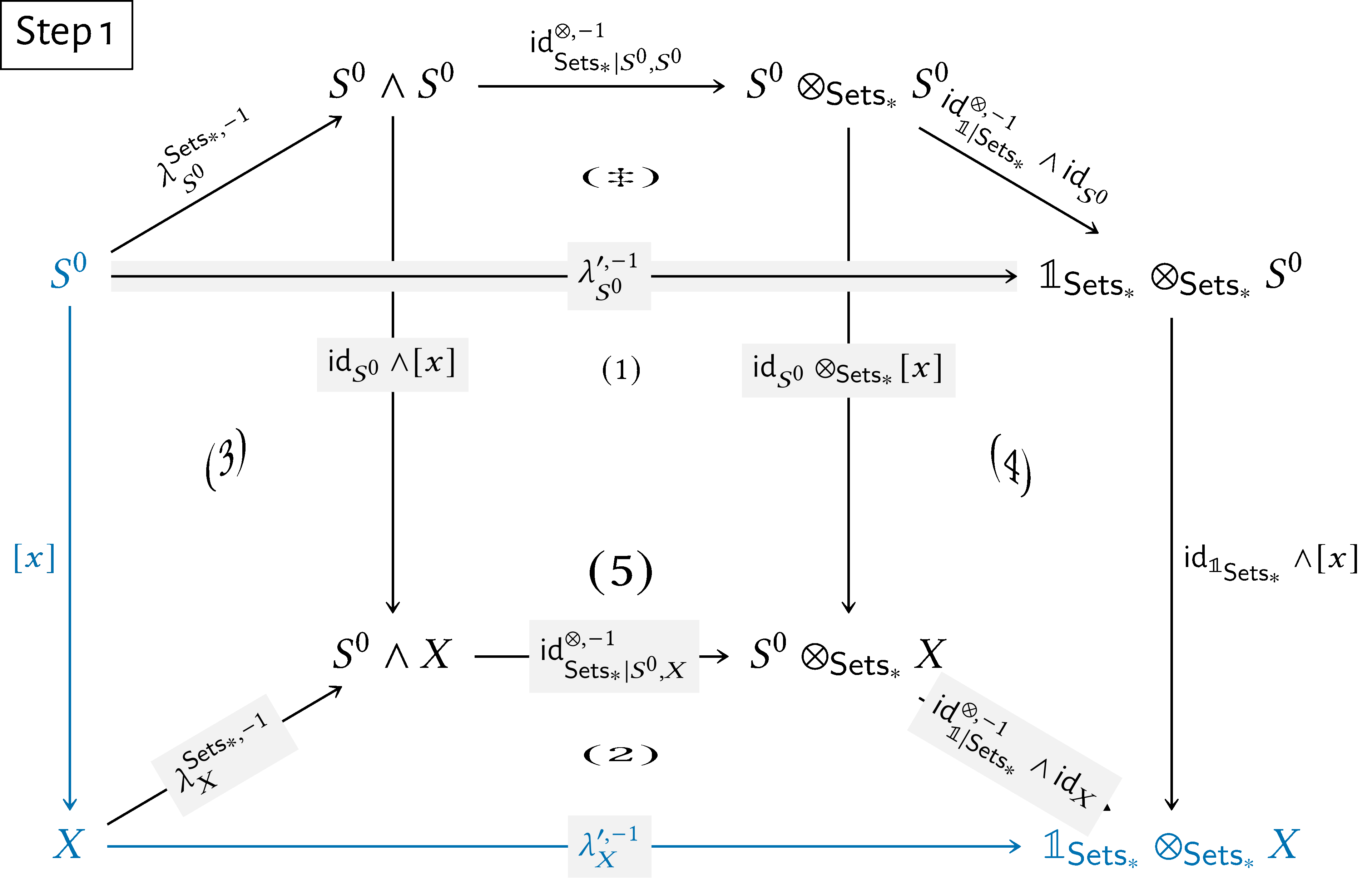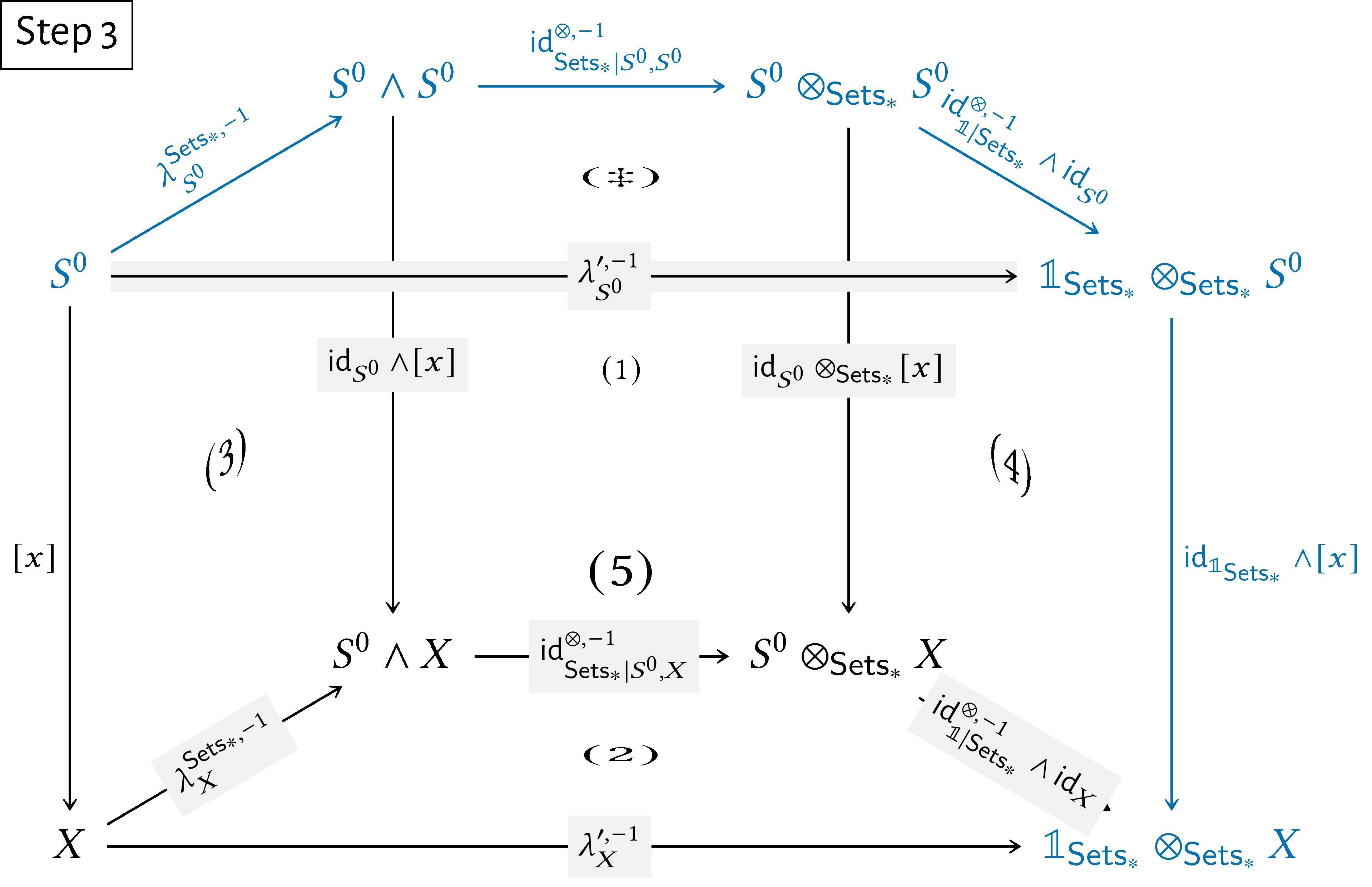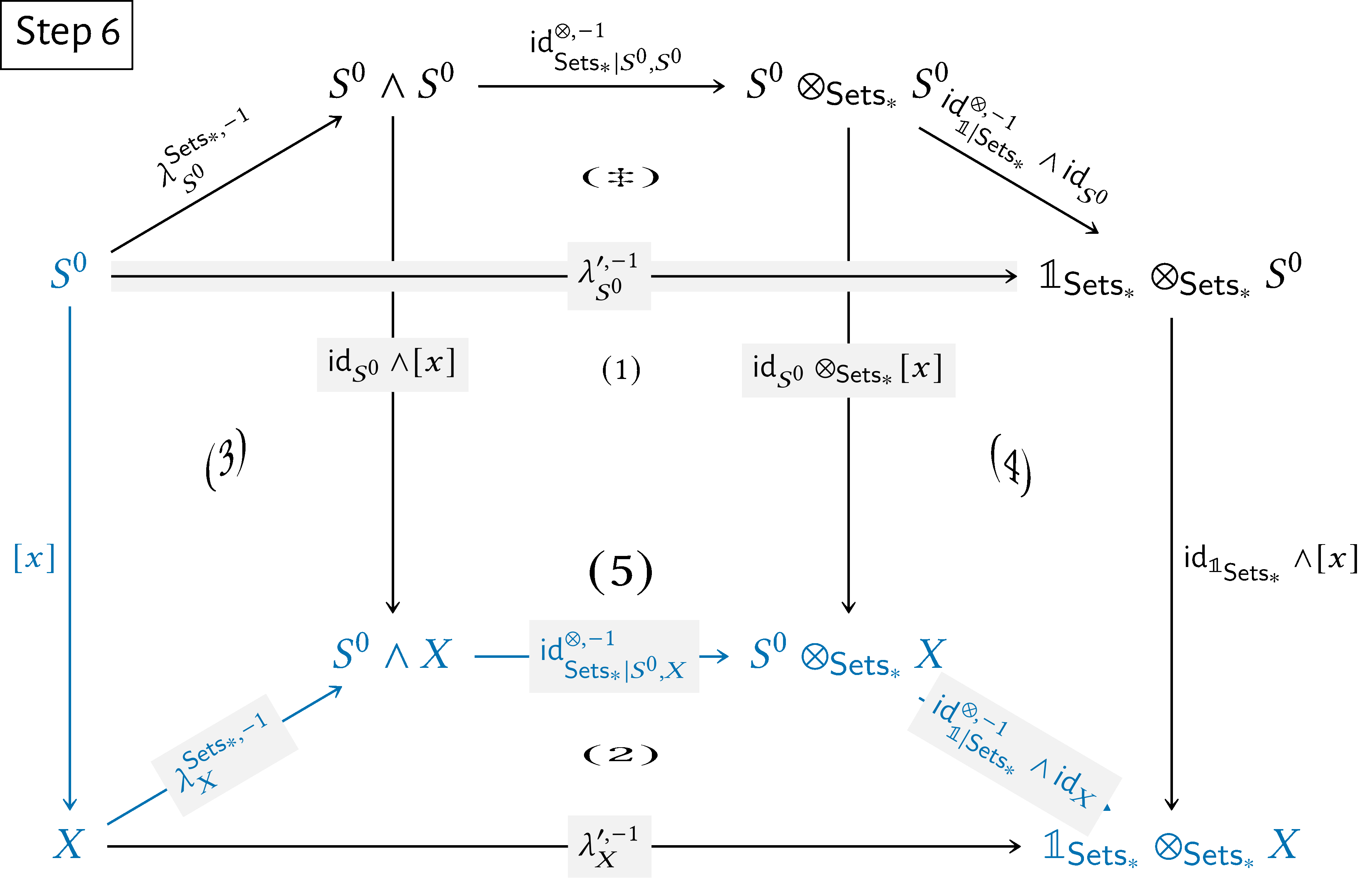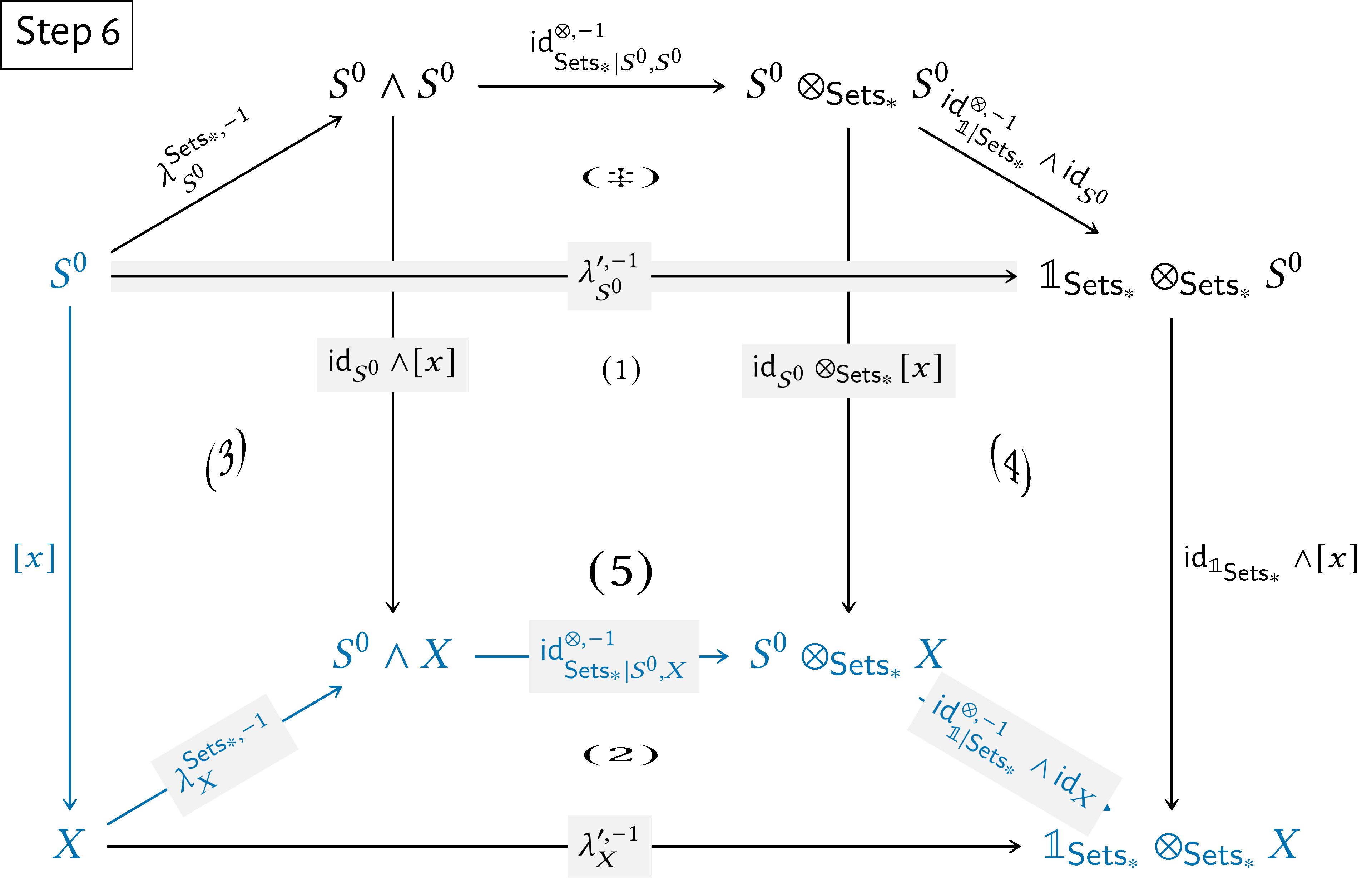
also commutes. Now, let $X\in \operatorname {\mathrm{Obj}}(\mathsf{Sets}_{*})$, let $x\in X$, and consider the diagram Since:
-
•
Subdiagram $(5)$ commutes by the naturality of $\lambda ^{\prime ,-1}$.
-
•
Subdiagram $(\ddagger )$ commutes, as proved above.
-
•
Subdiagram $(4)$ commutes by the naturality of $\operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathbb {1}|\mathsf{Sets}_{*}}$.
-
•
Subdiagram $(1)$ commutes by the naturality of $\operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathsf{Sets}_{*}}$.
-
•
Subdiagram $(3)$ commutes by the naturality of $\lambda ^{\mathsf{Sets}_{*},-1}$.
it follows that the diagram
Here’s a step-by-step showcase of this argument:
\begin{align*} \lambda ^{\prime ,-1}_{X}(x) & = [\lambda ^{\prime ,-1}_{X}\circ [x]](1)\\ & = [(\operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathbb {1}|\mathsf{Sets}_{*}}\wedge \operatorname {\mathrm{id}}_{X})\circ \operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathsf{Sets}_{*}|S^{0},X}\circ \lambda ^{\mathsf{Sets}_{*},-1}_{X}\circ [x]](1)\\ & = [(\operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathbb {1}|\mathsf{Sets}_{*}}\wedge \operatorname {\mathrm{id}}_{X})\circ \operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathsf{Sets}_{*}|S^{0},X}\circ \lambda ^{\mathsf{Sets}_{*},-1}_{X}](x) \end{align*}
for each $x\in X$, and thus we have
\[ \lambda ^{\prime ,-1}_{X}=(\operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathbb {1}|\mathsf{Sets}_{*}}\wedge \operatorname {\mathrm{id}}_{X})\circ \operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathsf{Sets}_{*}|S^{0},X}\circ \lambda ^{\mathsf{Sets}_{*},-1}_{X}. \]
Taking inverses then gives
\[ \lambda ^{\prime }_{X}=\lambda ^{\mathsf{Sets}_{*}}_{X}\circ \operatorname {\mathrm{id}}^{\otimes }_{\mathsf{Sets}_{*}|S^{0},X}\circ (\operatorname {\mathrm{id}}^{\otimes }_{\mathbb {1}|\mathsf{Sets}_{*}}\wedge \operatorname {\mathrm{id}}_{X}), \]
showing that the diagram
indeed commutes.
Braidedness of the Isomorphism $\mathord {\otimes _{\mathsf{Sets}_{*}}}\cong \mathord {\wedge }$
We have to show that the diagram commutes. To this end, we will first show that the diagram commutes. To that end, we will first show that the diagram commutes, and, to this end, we will first show that the diagram commutes. Indeed, consider the diagram whose boundary diagram corresponds to diagram $(\S )$ above. Since:
-
•
Subdiagram $(1)$ commutes by the naturality of $\operatorname {\mathrm{id}}^{\otimes }_{\mathsf{Sets}_{*}}$;
-
•
Subdiagrams $(2)$ and $(3)$ commute by the functoriality of $\otimes $;
-
•
Subdiagram $(4)$ commutes by the left monoidal unity of $(\operatorname {\mathrm{id}}^{\otimes },\operatorname {\mathrm{id}}^{\otimes }_{\mathbb {1}})$, which we proved above;
-
•
Subdiagram $(5)$ commutes by the naturality of $\lambda '$;
-
•
Subdiagram $(6)$ commutes by the naturality of $\rho '$, where the equality $\rho '_{\mathbb {1}_{\mathsf{Sets}_{*}}}=\lambda '_{\mathbb {1}_{\mathsf{Sets}_{*}}}$ comes from  ;
;
it follows that the boundary diagram, i.e. diagram $(\S )$, also commutes. Next, consider the diagram
whose boundary diagram corresponds to the diagram $(\ddagger )$ above. Since:
-
•
Subdiagrams $(1)$ and $(6)$ commute by  ;
;
-
•
Subdiagram $(2)$ commutes by the naturality of $\operatorname {\mathrm{id}}^{\otimes }_{\mathsf{Sets}_{*}}$;
-
•
Subdiagram $(\S )$ commutes, as was shown above;
-
•
Subdiagram $(3)$ commutes by the naturality of $\lambda ^{\mathsf{Sets}_{*}}$;
-
•
Subdiagram $(4)$ commutes trivially;
-
•
Subdiagram $(5)$ commutes by Chapter 13: Constructions With Monoidal Categories, Item 2c of Item 2 of Proposition 13.1.1.1.4, whose proof uses only the left monoidal unity of $(\operatorname {\mathrm{id}}^{\otimes },\operatorname {\mathrm{id}}^{\otimes }_{\mathbb {1}})$, which has been proven above;
it follows that the boundary diagram, i.e. diagram $(\ddagger )$, also commutes. Next, consider the diagram
whose boundary diagram corresponds to the diagram $(\dagger )$. Since:
-
•
Subdiagram $(1)$ commutes by the naturality of $\operatorname {\mathrm{id}}^{\otimes }_{\mathsf{Sets}_{*}}$;
-
•
Subdiagram $(2)$ commutes by the naturality of $\sigma '$ and the fact that $\operatorname {\mathrm{id}}^{\otimes }_{\mathbb {1}}$ is invertible;
-
•
Subdiagram $(\ddagger )$ commutes as proved above;
-
•
Subdiagram $(3)$ commutes by the naturality of $\sigma ^{\mathsf{Sets}_{*}}$ and the fact that $\operatorname {\mathrm{id}}^{\otimes }_{\mathbb {1}}$ is invertible;
-
•
Subdiagram $(4)$ commutes by the naturality of $\operatorname {\mathrm{id}}^{\otimes }_{\mathsf{Sets}_{*}}$;
it follows that the boundary diagram, i.e. diagram $(\dagger )$ also commutes. Taking inverses for the diagram $(\dagger )$, we see that the diagram
commutes as well. Now, let $X,Y\in \operatorname {\mathrm{Obj}}(\mathsf{Sets}_{*})$, let $x\in X$, let $y\in Y$, and consider the diagram which we partition into subdiagrams as follows: Since:
-
•
Subdiagram $(2)$ commutes by the naturality of $\sigma ^{\mathsf{Sets}_{*},-1}$.
-
•
Subdiagram $(5)$ commutes by the naturality of $\operatorname {\mathrm{id}}^{\otimes ,-1}$.
-
•
Subdiagram $(¶)$ commutes, as proved above.
-
•
Subdiagram $(4)$ commutes by the naturality of $\sigma ^{\prime ,-1}$.
-
•
Subdiagram $(1)$ commutes by the naturality of $\operatorname {\mathrm{id}}^{\otimes ,-1}$.
it follows that the diagram
commutes. We then have
\begin{align*} [\operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathsf{Sets}_{*}|X,Y}\circ \sigma ^{\mathsf{Sets}_{*},-1}_{X,Y}](y,x) & = [\operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathsf{Sets}_{*}|X,Y}\circ \sigma ^{\mathsf{Sets}_{*},-1}_{X,Y}\circ ([y]\wedge [x])](1,1)\\ & = [\sigma ^{\prime ,-1}_{X,Y}\circ \operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathsf{Sets}_{*}|Y,X}\circ ([y]\wedge [x])](1,1)\\ & = [\sigma ^{\prime ,-1}_{X,Y}\circ \operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathsf{Sets}_{*}|Y,X}](y,x) \end{align*}
for each $(y,x)\in Y\wedge X$, and thus we have
\[ \operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathsf{Sets}_{*}|X,Y}\circ \sigma ^{\mathsf{Sets}_{*},-1}_{X,Y}=\sigma ^{\prime ,-1}_{X,Y}\circ \operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathsf{Sets}_{*}|Y,X}. \]
Taking inverses then gives
\[ \sigma ^{\mathsf{Sets}_{*}}_{X,Y}\circ \operatorname {\mathrm{id}}^{\otimes }_{\mathsf{Sets}_{*}|X,Y}=\operatorname {\mathrm{id}}^{\otimes }_{\mathsf{Sets}_{*}|Y,X}\circ \sigma ^{\prime }_{X,Y}, \]
showing that the diagram
indeed commutes.
Monoidal Right Unity of the Isomorphism $\mathord {\otimes _{\mathsf{Sets}_{*}}}\cong \mathord {\wedge }$
We have to show that the diagram commutes. To this end, we will first show that the diagram corresponding to the case $X=S^{0}$, commutes. First, notice that we may write
\[ \sigma '_{S^{0},\mathbb {1}_{\mathsf{Sets}_{*}}}\colon S^{0}\otimes _{\mathsf{Sets}_{*}}\mathbb {1}_{\mathsf{Sets}_{*}}\to \mathbb {1}_{\mathsf{Sets}_{*}}\otimes _{\mathsf{Sets}_{*}}S^{0} \]
as the composition
Indeed, we may write this composition as part of the diagram which commutes since:
-
•
Subdiagram $(1)$ commutes by the braidedness of $\operatorname {\mathrm{id}}^{\otimes }$, as proved above.
-
•
Subdiagram $(2)$ commutes by  .
.
Next, consider the diagram
whose boundary diagram corresponds to the diagram $(\dagger )$ above, since the composition in red is equal to $\sigma '_{S^{0},\mathbb {1}_{\mathsf{Sets}_{*}}}$ as proved above, and then the composition in red composed with $\lambda '_{S^{0}}$ is equal to $\rho '_{S^{0}}$ by  . In this diagram:
. In this diagram:
-
•
Subdiagrams $(1)$, $(2)$, and $(3)$ commute by the naturality of $\operatorname {\mathrm{id}}^{\otimes }_{\mathsf{Sets}_{*}}$.
-
•
Subdiagrams $(4)$, $(5)$, and $(6)$ commute by the naturality of $\lambda ^{\mathsf{Sets}_{*}}$, where the equality $\lambda ^{\mathsf{Sets}_{*}}_{S^{0}}=\rho ^{\mathsf{Sets}_{*}}_{S^{0}}$ comes from  .
.
Since all subdiagrams commute, so does the boundary diagram, i.e. the diagram $(\dagger )$ above. As a result, the diagram
also commutes. Now, let $X\in \operatorname {\mathrm{Obj}}(\mathsf{Sets}_{*})$, let $x\in X$, and consider the diagram Since:
-
•
Subdiagram $(5)$ commutes by the naturality of $\rho ^{\prime ,-1}$.
-
•
Subdiagram $(\dagger )$ commutes, as proved above.
-
•
Subdiagram $(4)$ commutes by the naturality of $\operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathbb {1}|\mathsf{Sets}_{*}}$.
-
•
Subdiagram $(1)$ commutes by the naturality of $\operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathsf{Sets}_{*}}$.
-
•
Subdiagram $(3)$ commutes by the naturality of $\rho ^{\mathsf{Sets}_{*},-1}$.
it follows that the diagram
Here’s a step-by-step showcase of this argument:
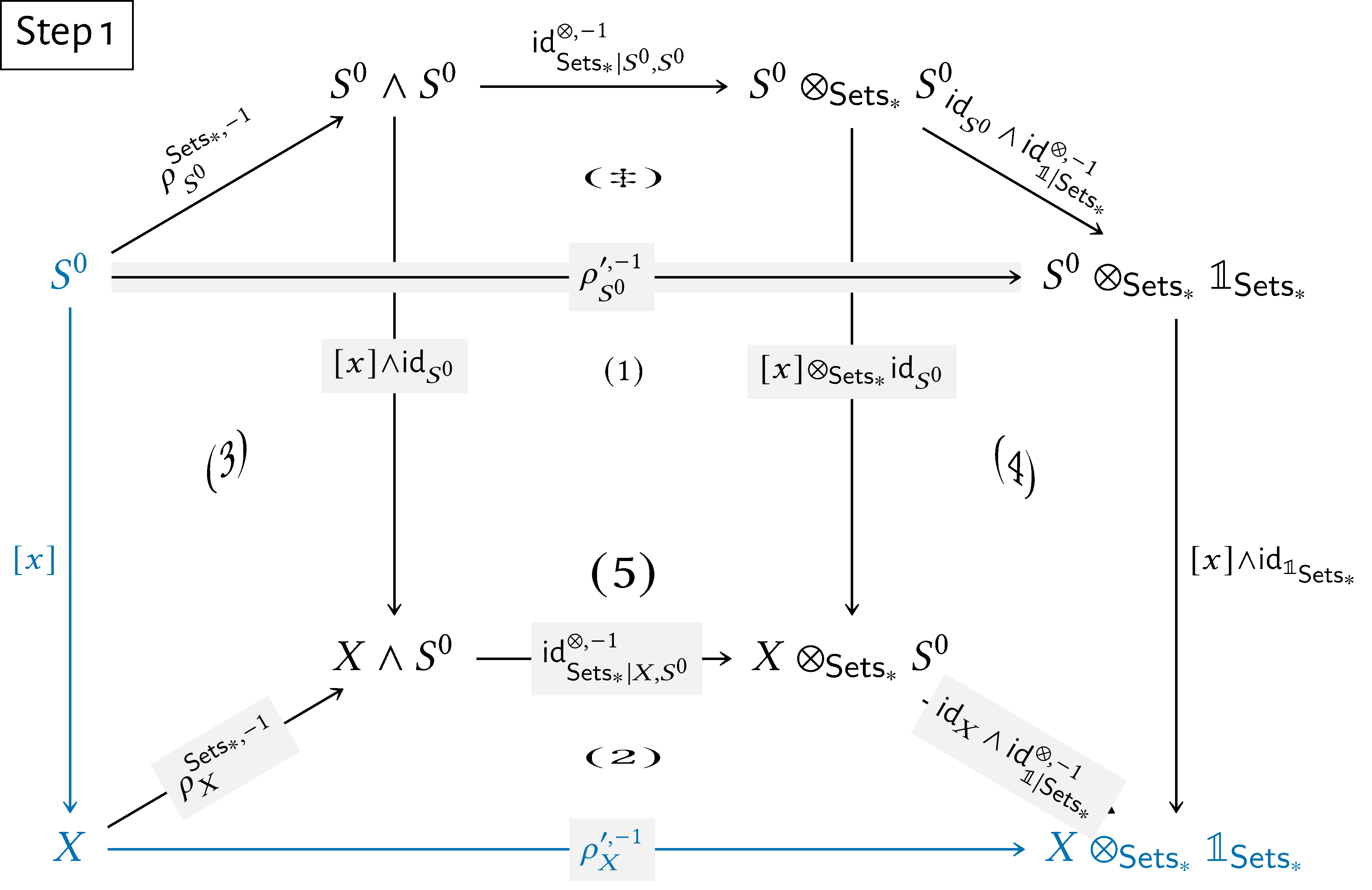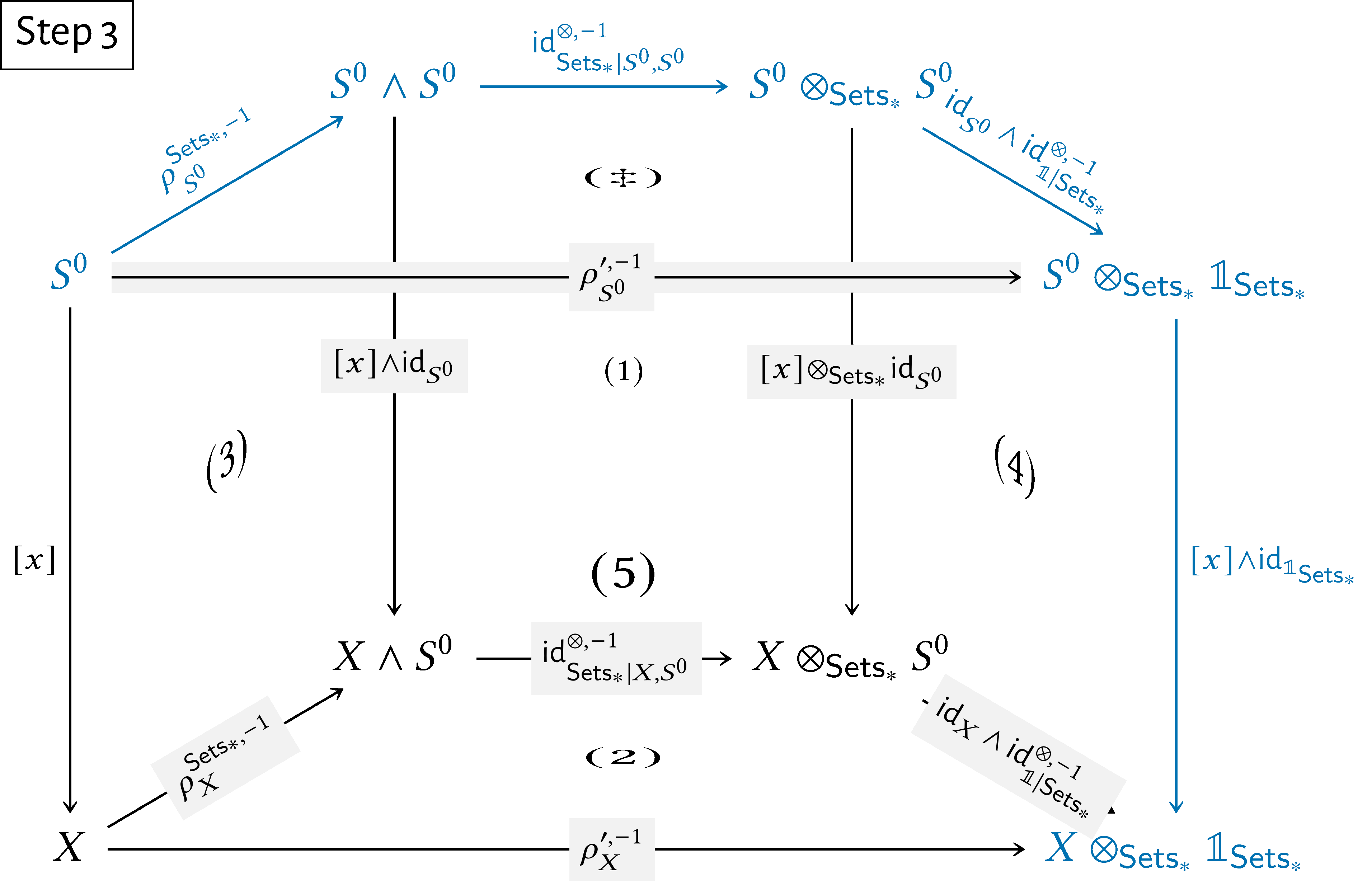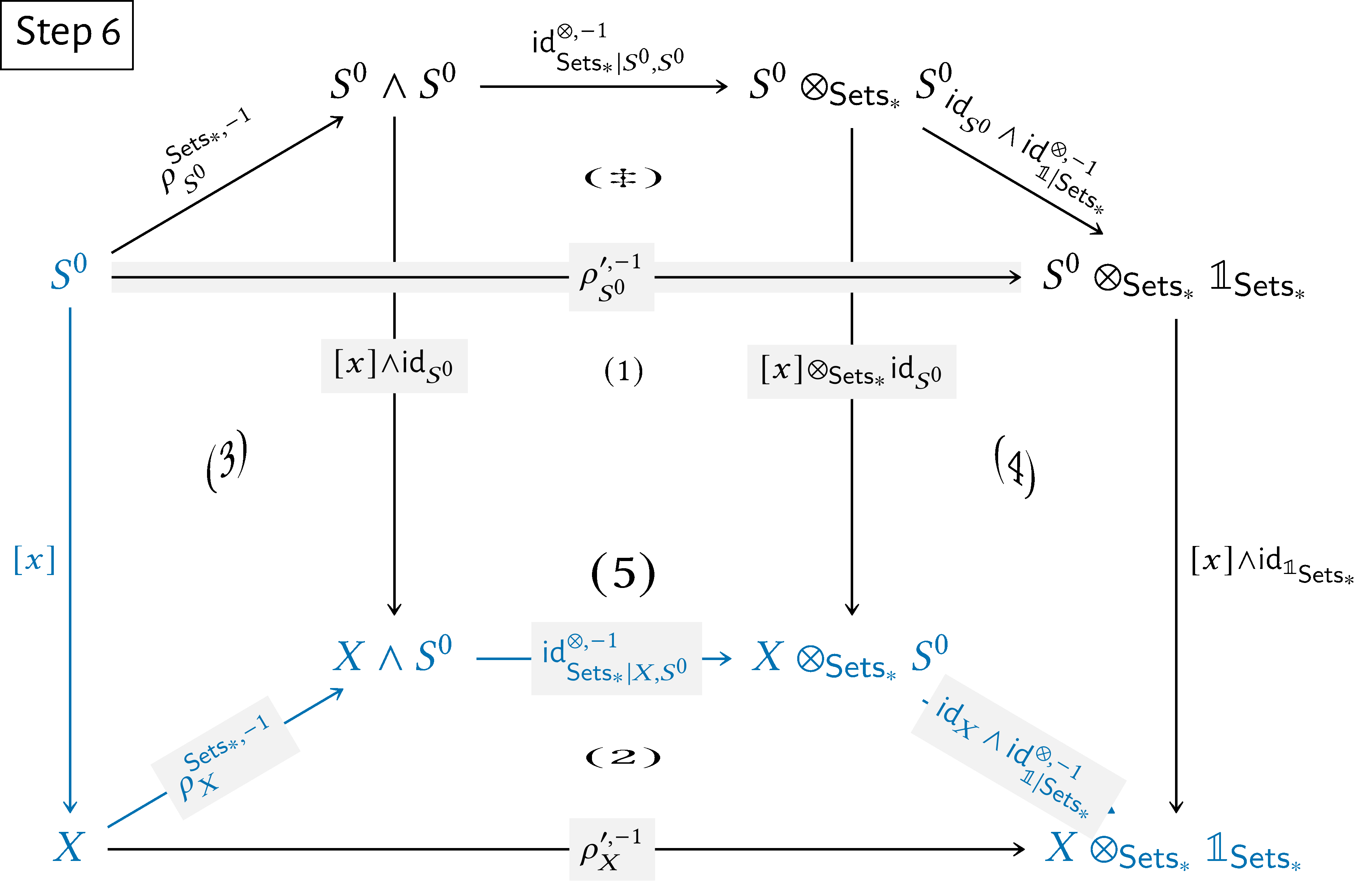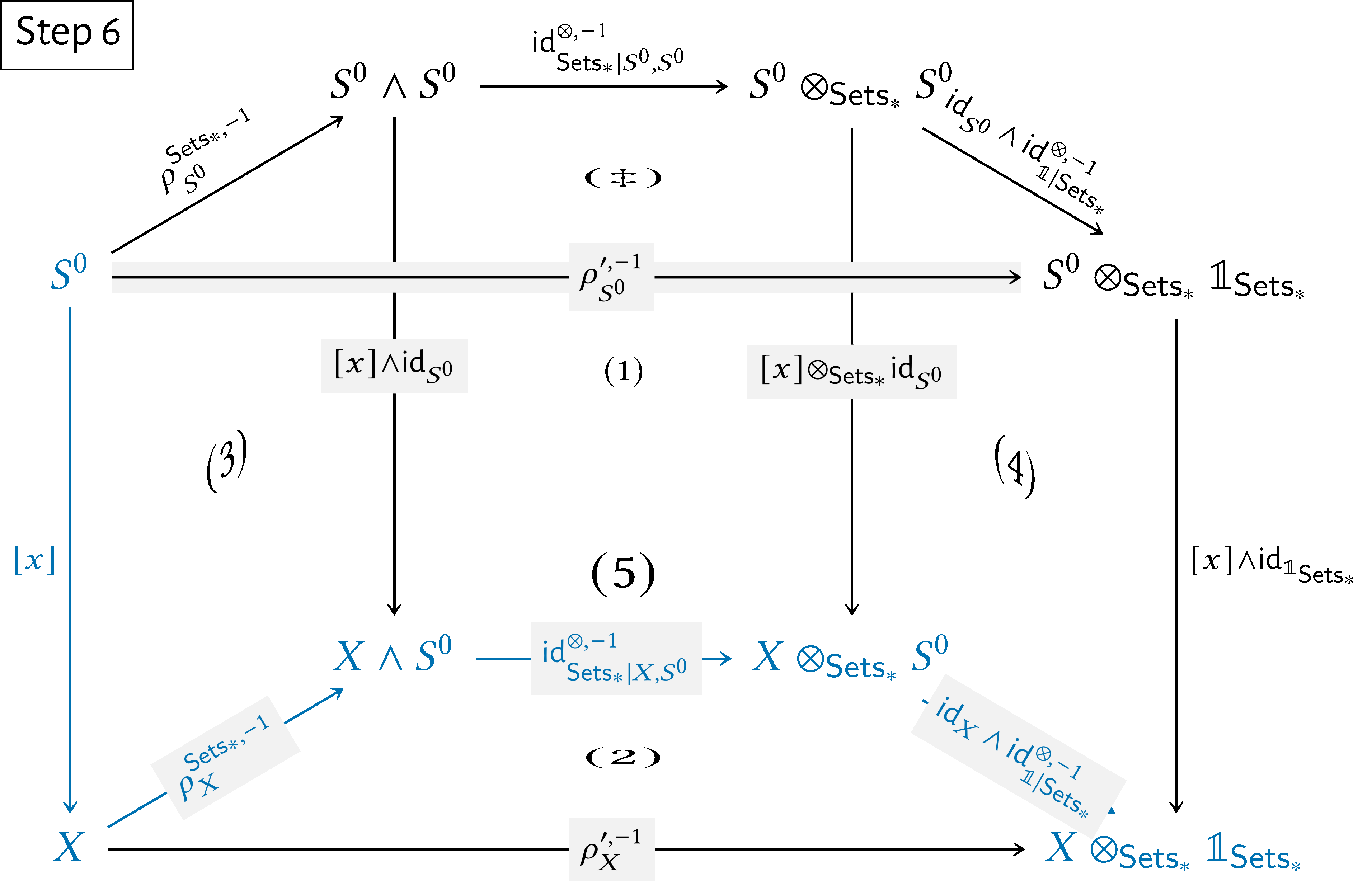
\begin{align*} \rho ^{\prime ,-1}_{X}(a) & = [\rho ^{\prime ,-1}_{X}\circ [x]](1)\\ & = [(\operatorname {\mathrm{id}}_{X}\wedge \operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathbb {1}|\mathsf{Sets}_{*}})\circ \operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathsf{Sets}_{*}|S^{0},X}\circ \rho ^{\mathsf{Sets}_{*},-1}_{X}\circ [x]](1)\\ & = [(\operatorname {\mathrm{id}}_{X}\wedge \operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathbb {1}|\mathsf{Sets}_{*}})\circ \operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathsf{Sets}_{*}|S^{0},X}\circ \rho ^{\mathsf{Sets}_{*},-1}_{X}](a) \end{align*}
for each $a\in X$, and thus we have
\[ \rho ^{\prime ,-1}_{X}=(\operatorname {\mathrm{id}}_{X}\wedge \operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathbb {1}|\mathsf{Sets}_{*}})\circ \operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathsf{Sets}_{*}|S^{0},X}\circ \rho ^{\mathsf{Sets}_{*},-1}_{X}. \]
Taking inverses then gives
\[ \rho ^{\prime }_{X}=\rho ^{\mathsf{Sets}_{*}}_{X}\circ \operatorname {\mathrm{id}}^{\otimes }_{\mathsf{Sets}_{*}|S^{0},X}\circ (\operatorname {\mathrm{id}}_{X}\wedge \operatorname {\mathrm{id}}^{\otimes }_{\mathbb {1}|\mathsf{Sets}_{*}}), \]
showing that the diagram
indeed commutes.
Monoidality of the Isomorphism $\mathord {\otimes _{\mathsf{Sets}_{*}}}\cong \mathord {\wedge }$
We have to show that the diagram commutes. To this end, we will first prove that the diagram commutes, and, to that end, we will first show that the diagram commutes. Indeed, consider the diagram whose boundary diagram corresponds to diagram $(\ddagger )$ above. Since:
-
•
Subdiagrams $(1)$, $(4)$, $(5)$, $(8)$, and $(11)$ commute by the naturality of $\operatorname {\mathrm{id}}^{\otimes }_{\mathsf{Sets}_{*}}$;
-
•
Subdiagram $(2)$ commutes by the right monoidal unity of $(\operatorname {\mathrm{id}}^{\otimes }_{\mathsf{Sets}_{*}},\operatorname {\mathrm{id}}^{\otimes }_{\mathbb {1}|\mathsf{Sets}_{*}})$;
-
•
Subdiagram $(3)$ commutes by the triangle identity for $(\alpha ',\lambda ',\rho ')$;
-
•
Subdiagram $(6)$ commutes by  ;
;
-
•
Subdiagram $(7)$ commutes by the naturality of $\rho ^{\mathsf{Sets}_{*}}$;
-
•
Subdiagram $(9)$ commutes by  ;
;
-
•
Subdiagram $(10)$ commutes by  ;
;
it follows that the boundary diagram, i.e. diagram $(\ddagger )$, also commutes. Consider now the diagram
whose boundary corresponds to diagram $(\dagger )$ above. Since:
-
•
Subdiagrams $(1)$, $(3)$, $(4)$, and $(6)$ commute by the naturality of $\operatorname {\mathrm{id}}^{\otimes }_{Sets_{*}}$;
-
•
Subdiagram $(\ddagger )$ commutes, as proved above;
-
•
Subdiagram $(2)$ commutes by the naturality of $\alpha '$;
-
•
Subdiagram $(5)$ commutes by the naturality of $\alpha ^{\mathsf{Sets}_{*}}$;
it follows that the boundary diagram, i.e. diagram $(\dagger )$, also commutes. Taking inverses on the diagram $(\dagger )$, we see that the diagram
commutes as well. Now, let $X,Y,Z\in \operatorname {\mathrm{Obj}}(\mathsf{Sets}_{*})$, let $x\in X$, let $y\in Y$, let $z\in Z$, and consider the diagram which we partition into subdiagrams as follows: Since:
-
•
Subdiagram $(1)$ commutes by the naturality of $\alpha ^{\mathsf{Sets}_{*},-1}$.
-
•
Subdiagram $(2)$ commutes by the naturality of $\operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathsf{Sets}_{*}}$.
-
•
Subdiagram $(3)$ commutes by the naturality of $\operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathsf{Sets}_{*}}$.
-
•
Subdiagram $(\dagger )$ commutes, as proved above.
-
•
Subdiagram $(4)$ commutes by the naturality of $\operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathsf{Sets}_{*}}$.
-
•
Subdiagram $(5)$ commutes by the naturality of $\operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathsf{Sets}_{*}}$.
-
•
Subdiagram $(6)$ commutes by the naturality of $\alpha ^{\prime ,-1}$.
it follows that the diagram
also commutes. We then have
\begin{align*} \left[(\operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathsf{Sets}_{*}|X,Y}\otimes _{\mathsf{Sets}_{*}}\operatorname {\mathrm{id}}_{Z})\circ \operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathsf{Sets}_{*}|X\wedge Y,Z}\right.\\ \left.{}\circ \alpha ^{\mathsf{Sets}_{*},-1}_{X,Y,Z}\right](x,(y,z)) & = \left[(\operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathsf{Sets}_{*}|X,Y}\otimes _{\mathsf{Sets}_{*}}\operatorname {\mathrm{id}}_{Z})\circ \operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathsf{Sets}_{*}|X\wedge Y,Z}\right.\\ & \phantom{={}} \mkern 4mu\left.{}{}\circ \alpha ^{\mathsf{Sets}_{*},-1}_{X,Y,Z}\circ ([x]\wedge ([y]\wedge [z]))\right](1,(1,1))\\ & = \left[\alpha ^{\prime ,-1}_{X,Y,Z}\circ (\operatorname {\mathrm{id}}_{X}\wedge \operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathsf{Sets}_{*}|Y,Z})\right.\\ & \phantom{={}} \mkern 4mu\left.{}\circ \operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathsf{Sets}_{*}|X,Y\wedge Z}\circ ([x]\wedge ([y]\wedge [z]))\right](1,(1,1))\\ & = [\alpha ^{\prime ,-1}_{X,Y,Z}\circ (\operatorname {\mathrm{id}}_{X}\wedge \operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathsf{Sets}_{*}|Y,Z})\circ \operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathsf{Sets}_{*}|X,Y\wedge Z}](x,(y,z)) \end{align*}
for each $(x,(y,z))\in X\wedge (Y\wedge Z)$, and thus we have
\[ (\operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathsf{Sets}_{*}|X,Y}\otimes _{\mathsf{Sets}_{*}}\operatorname {\mathrm{id}}_{Z})\circ \operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathsf{Sets}_{*}|X\wedge Y,Z}\circ \alpha ^{\mathsf{Sets}_{*},-1}_{X,Y,Z}=\alpha ^{\prime ,-1}_{X,Y,Z}\circ (\operatorname {\mathrm{id}}_{X}\wedge \operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathsf{Sets}_{*}|Y,Z})\circ \operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathsf{Sets}_{*}|X,Y\wedge Z}. \]
Taking inverses then gives
\[ \alpha ^{\mathsf{Sets}_{*}}_{X,Y,Z}\circ \operatorname {\mathrm{id}}^{\otimes }_{\mathsf{Sets}_{*}|X\wedge Y,Z}\circ (\operatorname {\mathrm{id}}^{\otimes }_{\mathsf{Sets}_{*}|X,Y}\otimes _{\mathsf{Sets}_{*}}\operatorname {\mathrm{id}}_{Z})=\operatorname {\mathrm{id}}^{\otimes }_{\mathsf{Sets}_{*}|X,Y\wedge Z}\circ (\operatorname {\mathrm{id}}_{X}\wedge \operatorname {\mathrm{id}}^{\otimes }_{\mathsf{Sets}_{*}|Y,Z})\circ \alpha ^{\prime }_{X,Y,Z}, \]
showing that the diagram indeed commutes.
Uniqueness of the Isomorphism $\mathord {\otimes _{\mathsf{Sets}_{*}}}\cong \mathord {\wedge }$
Let $\phi ,\psi \colon -_{1}\otimes _{\mathsf{Sets}_{*}}-_{2}\Rightarrow -_{1}\wedge -_{2}$ be natural isomorphisms. Since these isomorphisms are compatible with the unitors of $\mathsf{Sets}_{*}$ with respect to $\wedge $ and $\otimes $ (as shown above), we have
\begin{align*} \lambda '_{Y} & = \lambda ^{\mathsf{Sets}_{*}}_{Y}\circ \phi _{S^{0},Y}\circ (\operatorname {\mathrm{id}}^{\otimes }_{\mathbb {1}|\mathsf{Sets}}\otimes _{\mathsf{Sets}}\operatorname {\mathrm{id}}_{Y}),\\ \lambda '_{Y} & = \lambda ^{\mathsf{Sets}_{*}}_{Y}\circ \psi _{S^{0},Y}\circ (\operatorname {\mathrm{id}}^{\otimes }_{\mathbb {1}|\mathsf{Sets}}\otimes _{\mathsf{Sets}}\operatorname {\mathrm{id}}_{Y}). \end{align*}
Postcomposing both sides with $\lambda ^{\mathsf{Sets}_{*},-1}_{Y}$ and then precomposing both sides with $\operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathbb {1}|\mathsf{Sets}}\otimes _{\mathsf{Sets}}\operatorname {\mathrm{id}}_{Y}$ gives
\begin{align*} \lambda ^{\mathsf{Sets}_{*},-1}_{Y}\circ \lambda '_{Y}\circ (\operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathbb {1}|\mathsf{Sets}}\otimes _{\mathsf{Sets}}\operatorname {\mathrm{id}}_{Y}) & = \phi _{S^{0},Y},\\ \lambda ^{\mathsf{Sets}_{*},-1}_{Y}\circ \lambda '_{Y}\circ (\operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathbb {1}|\mathsf{Sets}}\otimes _{\mathsf{Sets}}\operatorname {\mathrm{id}}_{Y}) & = \psi _{S^{0},Y}, \end{align*}
and thus we have
\[ \phi _{S^{0},Y}=\psi _{S^{0},Y} \]
for each $Y\in \operatorname {\mathrm{Obj}}(\mathsf{Sets}_{*})$. Now, let $x\in X$ and consider the naturality diagrams
for $\phi $ and $\psi $ with respect to the morphisms $[x]$ and $\operatorname {\mathrm{id}}_{Y}$. Having shown that $\phi _{S^{0},Y}=\psi _{S^{0},Y}$, we have
\begin{align*} \phi _{X,Y}(x,y) & = [\phi _{X,Y}\circ ([x]\wedge \operatorname {\mathrm{id}}_{Y})](1,y)\\ & = [([x]\otimes _{\mathsf{Sets}_{*}}\operatorname {\mathrm{id}}_{Y})\circ \phi _{S^{0},Y}](1,y)\\ & = [([x]\otimes _{\mathsf{Sets}_{*}}\operatorname {\mathrm{id}}_{Y})\circ \psi _{S^{0},Y}](1,y)\\ & = [\psi _{X,Y}\circ ([x]\wedge \operatorname {\mathrm{id}}_{Y})](1,y)\\ & = \psi _{X,Y}(x,y) \end{align*}
for each $(x,y)\in X\wedge Y$. Therefore we have
\[ \phi _{X,Y}=\psi _{X,Y} \]
for each $X,Y\in \operatorname {\mathrm{Obj}}(\mathsf{Sets}_{*})$ and thus $\phi =\psi $, showing the isomorphism $\mathord {\otimes _{\mathsf{Sets}_{*}}}\cong \mathord {\times }$ to be unique.










