3.
Since $A\cong \mathchoice {\mathbin {\textstyle \coprod }}{\mathbin {\textstyle \coprod }}{\mathbin {\scriptstyle \textstyle \coprod }}{\mathbin {\scriptscriptstyle \textstyle \coprod }}_{a\in A}\mathrm{pt}$ and $\otimes _{\mathsf{Sets}}$ preserves colimits in each variable, we have
\begin{align*} A\otimes _{\mathsf{Sets}}B & \cong \webleft (\coprod _{a\in A}\mathrm{pt}\webright )\otimes _{\mathsf{Sets}}B\\ & \cong \coprod _{a\in A}\webleft (\mathrm{pt}\otimes _{\mathsf{Sets}}B\webright )\\ & \cong \coprod _{a\in A}B\\ & \cong A\times B, \end{align*}
naturally in $B\in \operatorname {\mathrm{Obj}}\webleft (\mathsf{Sets}\webright )$, where we have used that $\mathrm{pt}$ is the monoidal unit for $\otimes _{\mathsf{Sets}}$. Thus $A\otimes _{\mathsf{Sets}}-\cong A\times -$ for each $A\in \operatorname {\mathrm{Obj}}\webleft (\mathsf{Sets}\webright )$.
4.
Similarly, $-\otimes _{\mathsf{Sets}}B\cong -\times B$ for each $B\in \operatorname {\mathrm{Obj}}\webleft (\mathsf{Sets}\webright )$.
5.
By 
, we then have $\mathord {\otimes _{\mathsf{Sets}}}\cong \mathord {\times }$.
Below, we’ll show that if a natural isomorphism $\mathord {\otimes _{\mathsf{Sets}}}\cong \mathord {\times }$ exists, then it must be unique. This will show that the isomorphism constructed above is equal to the isomorphism $\operatorname {\mathrm{id}}^{\otimes }_{\mathsf{Sets}|A,B}\colon A\otimes _{\mathsf{Sets}}B\to A\times B$ from before.
Constructing an Isomorphism $\operatorname {\mathrm{id}}^{\otimes }_{\mathbb {1}}\colon \mathbb {1}_{\mathsf{Sets}}\to \mathrm{pt}$
We define an isomorphism $\operatorname {\mathrm{id}}^{\otimes }_{\mathbb {1}}\colon \mathbb {1}_{\mathsf{Sets}}\to \mathrm{pt}$ as the composition
\[ \mathbb {1}_{\mathsf{Sets}}\overset {\rho ^{\mathsf{Sets},-1}_{\mathbb {1}_{\mathsf{Sets}}}}{\underset {\scriptstyle \mathord {\sim }}{\dashrightarrow }}\mathbb {1}_{\mathsf{Sets}}\times \mathrm{pt}\overset {\operatorname {\mathrm{id}}^{\otimes }_{\mathsf{Sets}|\mathbb {1}_{\mathsf{Sets}}}}{\underset {\scriptstyle \mathord {\sim }}{\dashrightarrow }}\mathbb {1}_{\mathsf{Sets}}\otimes _{\mathsf{Sets}}\mathrm{pt}\overset {\lambda '_{\mathrm{pt}}}{\underset {\scriptstyle \mathord {\sim }}{\dashrightarrow }}\mathrm{pt} \]
in $\mathsf{Sets}$.
Monoidal Left Unity of the Isomorphism $\mathord {\otimes _{\mathsf{Sets}}}\cong \mathord {\times }$
We have to show that the diagram
commutes. First, note that the diagram
corresponding to the case $A=\mathrm{pt}$, commutes by the terminality of $\mathrm{pt}$ (
Chapter 4: Constructions With Sets,
Construction 4.1.1.1.2). Since this diagram commutes, so does the diagram
Now, let $A\in \operatorname {\mathrm{Obj}}\webleft (\mathsf{Sets}\webright )$, let $a\in A$, and consider the diagram
Since:
-
•
Subdiagram $\webleft (5\webright )$ commutes by the naturality of $\lambda ^{\prime ,-1}$.
-
•
Subdiagram $\webleft (\dagger \webright )$ commutes, as proved above.
-
•
Subdiagram $\webleft (4\webright )$ commutes by the naturality of $\operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathbb {1}|\mathsf{Sets}}$.
-
•
Subdiagram $\webleft (1\webright )$ commutes by the naturality of $\operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathsf{Sets}}$.
-
•
Subdiagram $\webleft (3\webright )$ commutes by the naturality of $\lambda ^{\mathsf{Sets},-1}$.
it follows that the diagram
Here’s a step-by-step showcase of this argument:
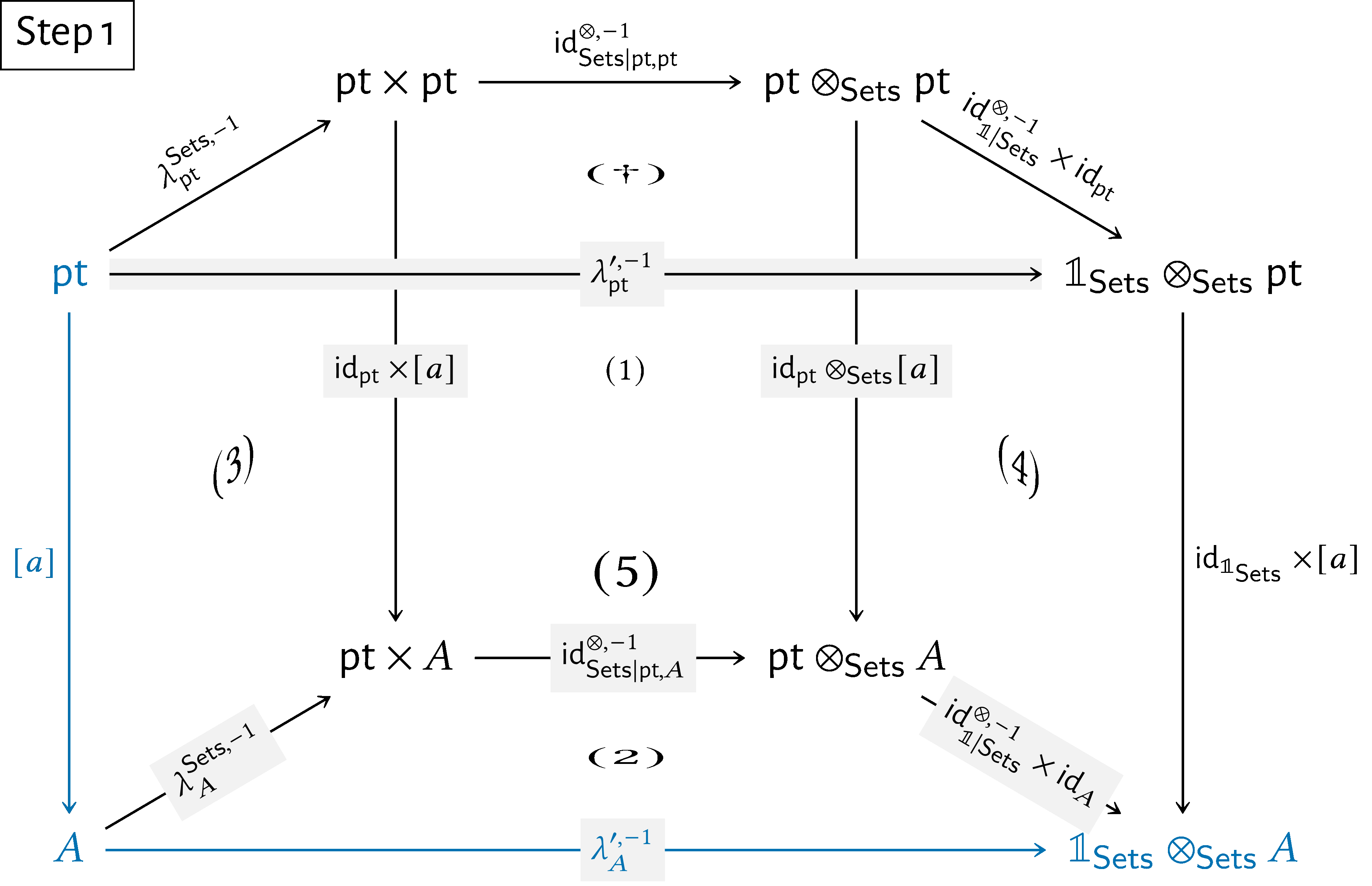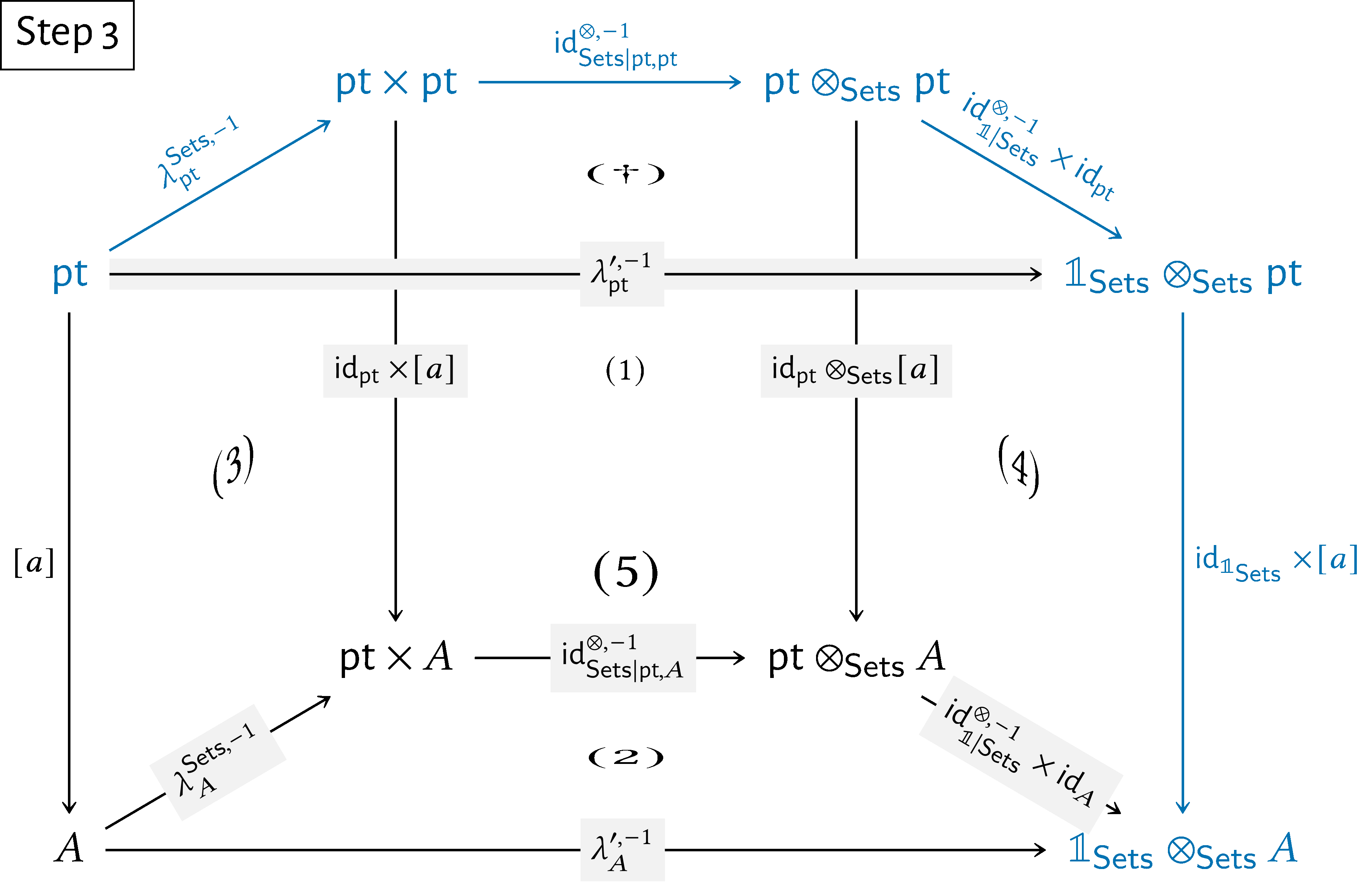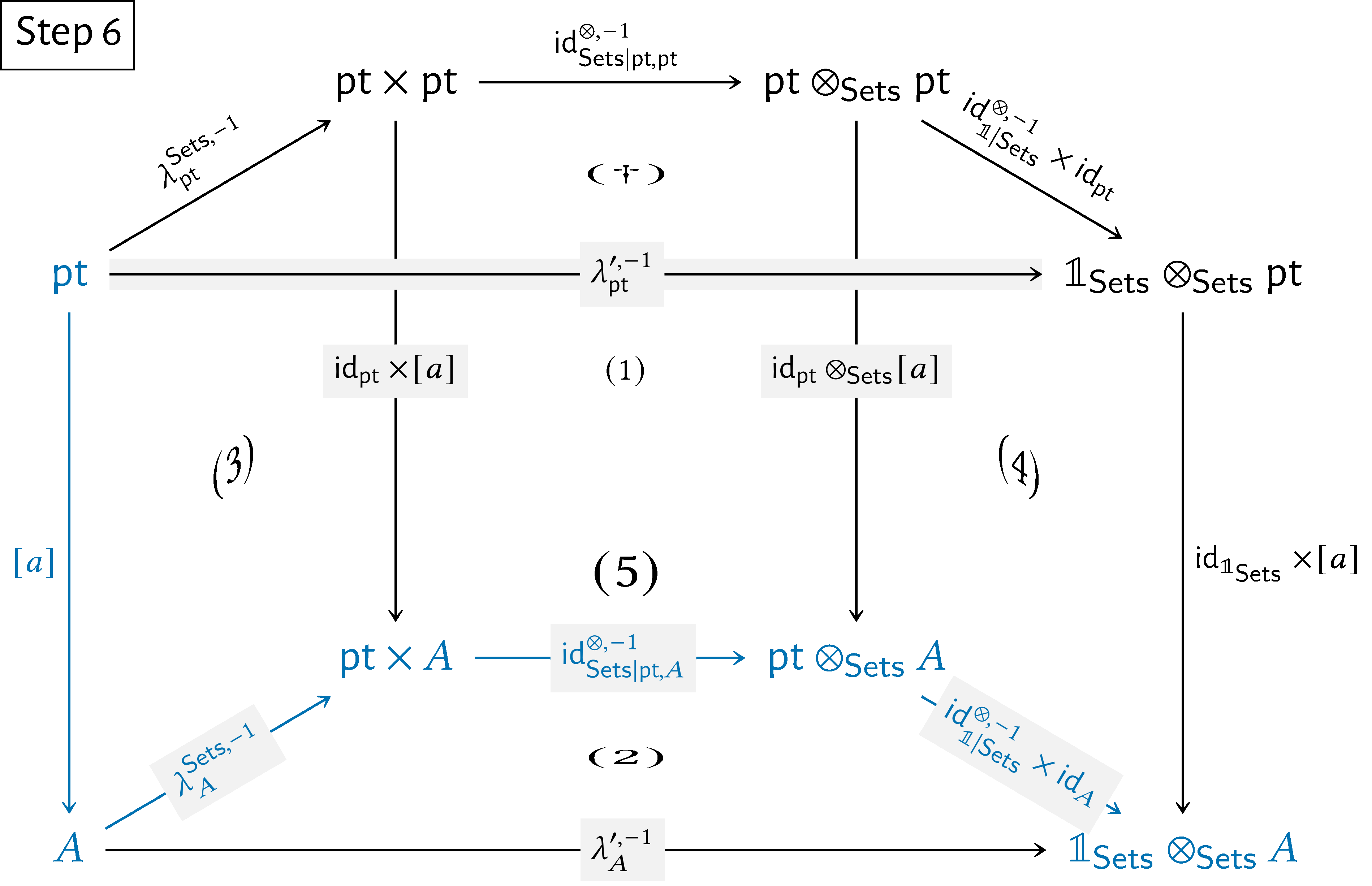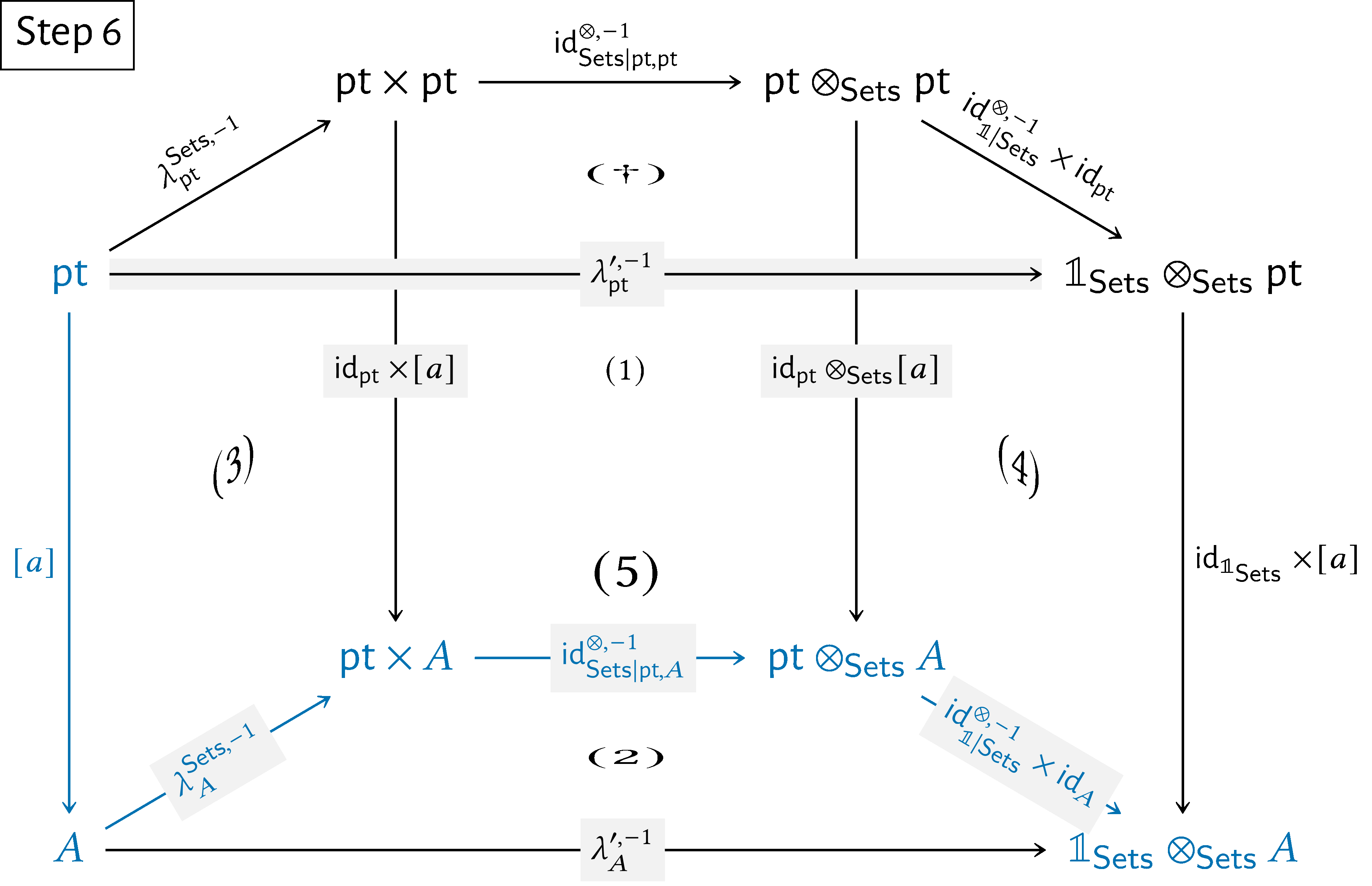
We then have
\begin{align*} \lambda ^{\prime ,-1}_{A}\webleft (a\webright ) & = \webleft [\lambda ^{\prime ,-1}_{A}\circ \webleft [a\webright ]\webright ]\webleft (\star \webright )\\ & = \webleft [\webleft (\operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathbb {1}|\mathsf{Sets}}\times \operatorname {\mathrm{id}}_{A}\webright )\circ \operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathsf{Sets}|\mathrm{pt},A}\circ \lambda ^{\mathsf{Sets},-1}_{A}\circ \webleft [a\webright ]\webright ]\webleft (\star \webright )\\ & = \webleft [\webleft (\operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathbb {1}|\mathsf{Sets}}\times \operatorname {\mathrm{id}}_{A}\webright )\circ \operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathsf{Sets}|\mathrm{pt},A}\circ \lambda ^{\mathsf{Sets},-1}_{A}\webright ]\webleft (a\webright ) \end{align*}
for each $a\in A$, and thus we have
\[ \lambda ^{\prime ,-1}_{A}=\webleft (\operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathbb {1}|\mathsf{Sets}}\times \operatorname {\mathrm{id}}_{A}\webright )\circ \operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathsf{Sets}|\mathrm{pt},A}\circ \lambda ^{\mathsf{Sets},-1}_{A}. \]
Taking inverses then gives
\[ \lambda ^{\prime }_{A}=\lambda ^{\mathsf{Sets}}_{A}\circ \operatorname {\mathrm{id}}^{\otimes }_{\mathsf{Sets}|\mathrm{pt},A}\circ \webleft (\operatorname {\mathrm{id}}^{\otimes }_{\mathbb {1}|\mathsf{Sets}}\times \operatorname {\mathrm{id}}_{A}\webright ), \]
showing that the diagram
indeed commutes.
Monoidal Right Unity of the Isomorphism $\mathord {\otimes _{\mathsf{Sets}}}\cong \mathord {\times }$
We can use the same argument we used to prove the monoidal left unity of the isomorphism $\mathord {\otimes _{\mathsf{Sets}}}\cong \mathord {\times }$ above. For completeness, we repeat it below.
We have to show that the diagram
commutes. First, note that the diagram
corresponding to the case $A=\mathrm{pt}$, commutes by the terminality of $\mathrm{pt}$ (
Chapter 4: Constructions With Sets,
Construction 4.1.1.1.2). Since this diagram commutes, so does the diagram
Now, let $A\in \operatorname {\mathrm{Obj}}\webleft (\mathsf{Sets}\webright )$, let $a\in A$, and consider the diagram
Since:
-
•
Subdiagram $\webleft (5\webright )$ commutes by the naturality of $\rho ^{\prime ,-1}$.
-
•
Subdiagram $\webleft (\dagger \webright )$ commutes, as proved above.
-
•
Subdiagram $\webleft (4\webright )$ commutes by the naturality of $\operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathbb {1}|\mathsf{Sets}}$.
-
•
Subdiagram $\webleft (1\webright )$ commutes by the naturality of $\operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathsf{Sets}}$.
-
•
Subdiagram $\webleft (3\webright )$ commutes by the naturality of $\rho ^{\mathsf{Sets},-1}$.
it follows that the diagram
Here’s a step-by-step showcase of this argument:
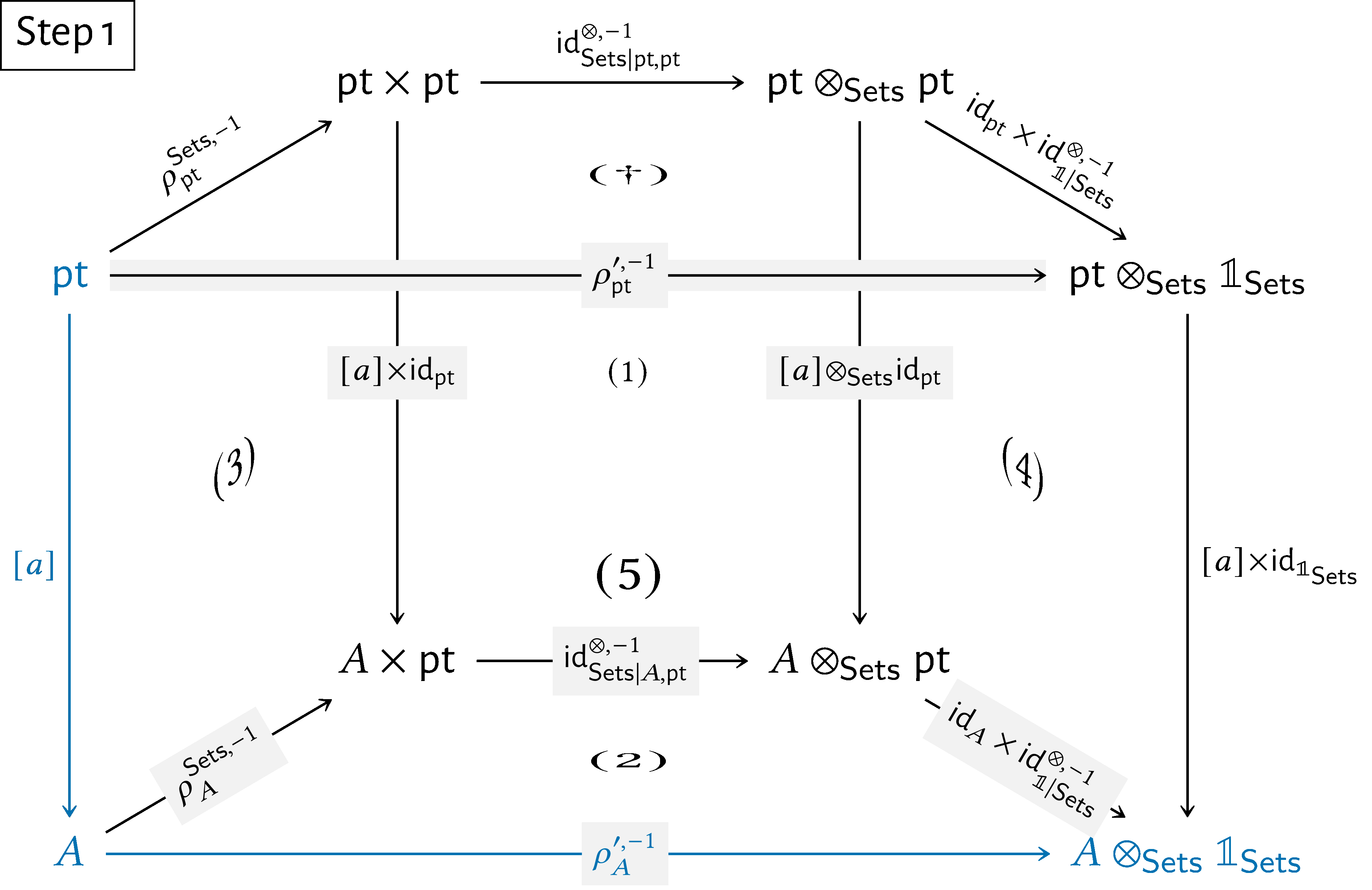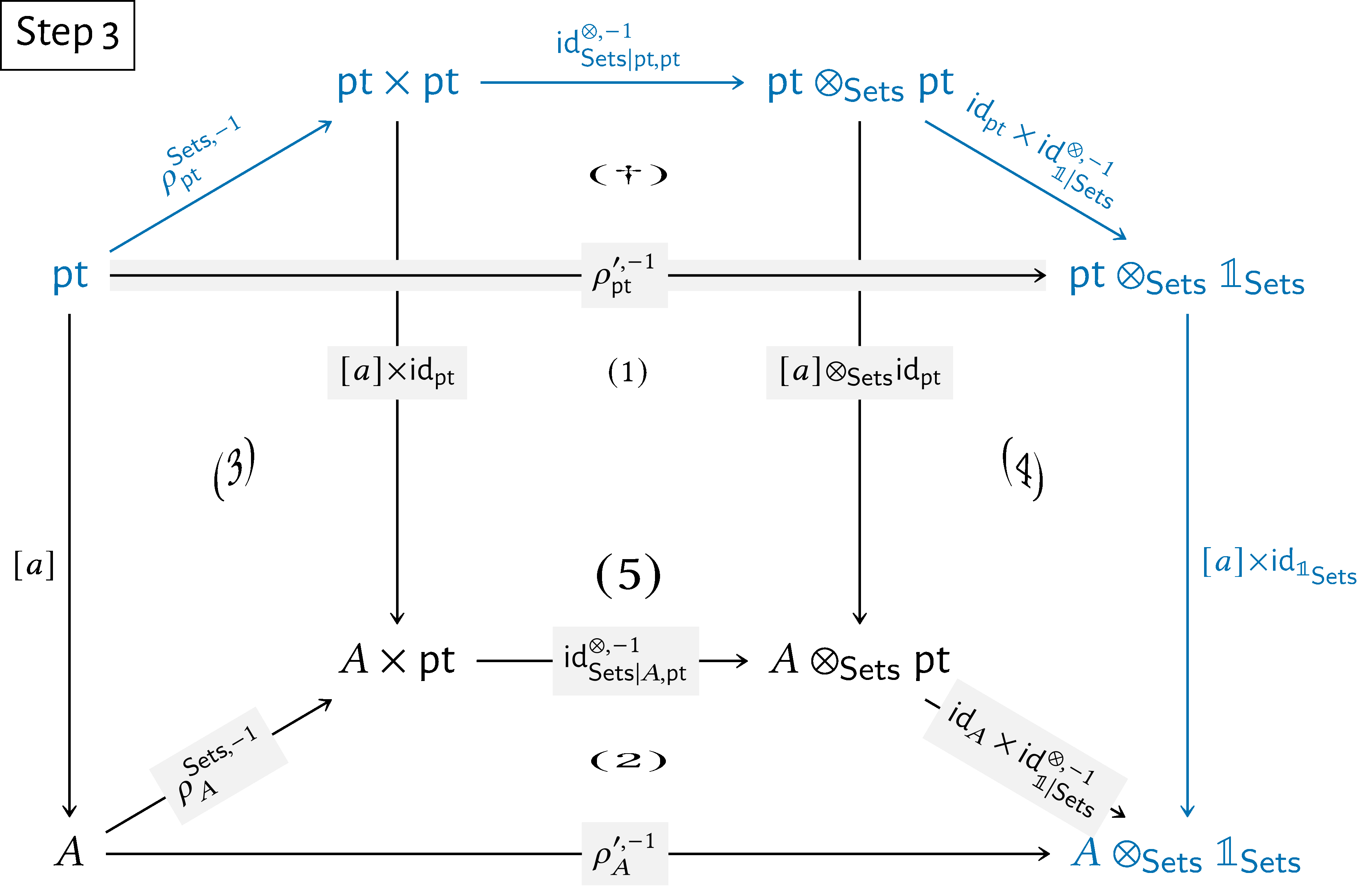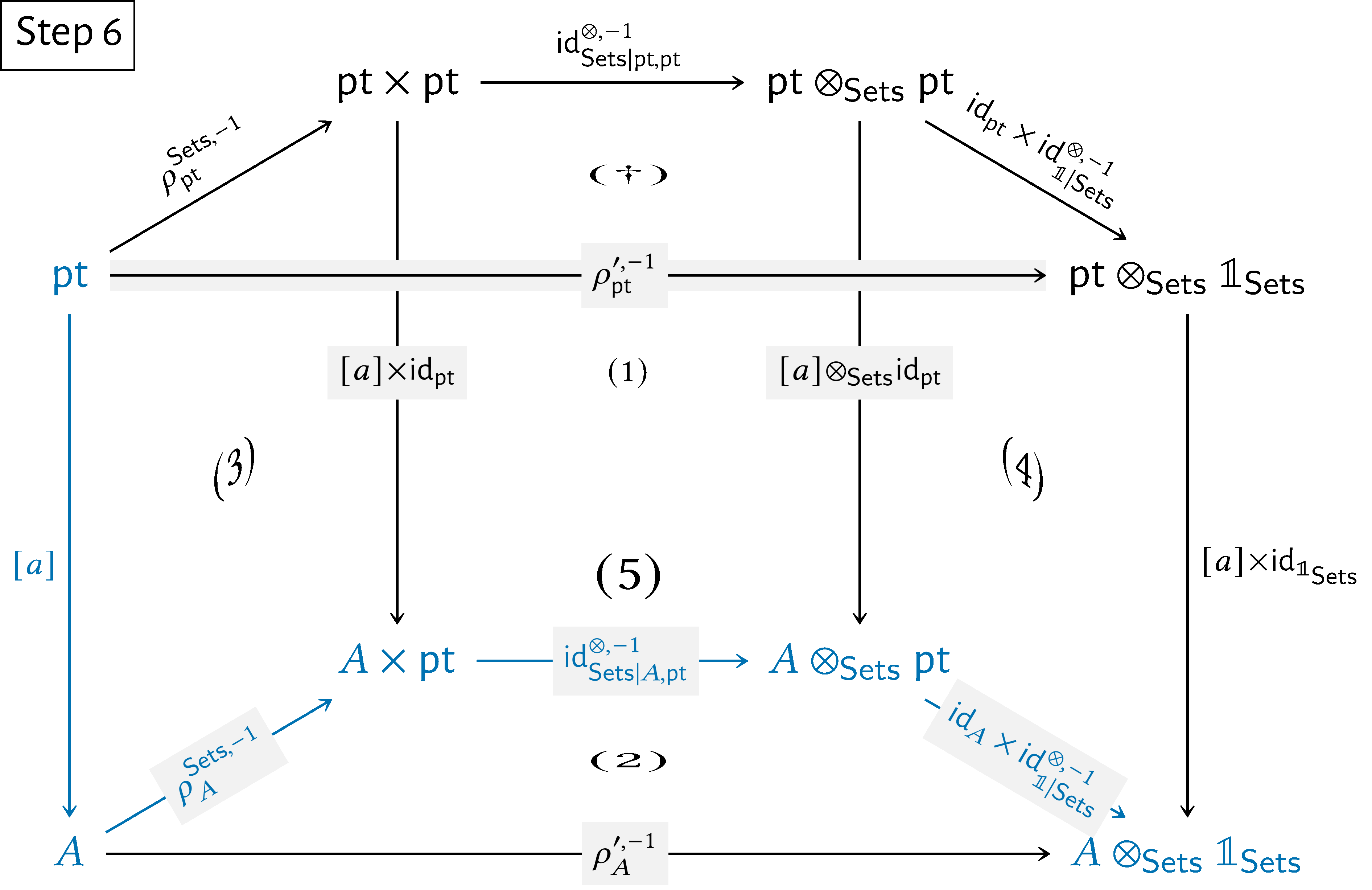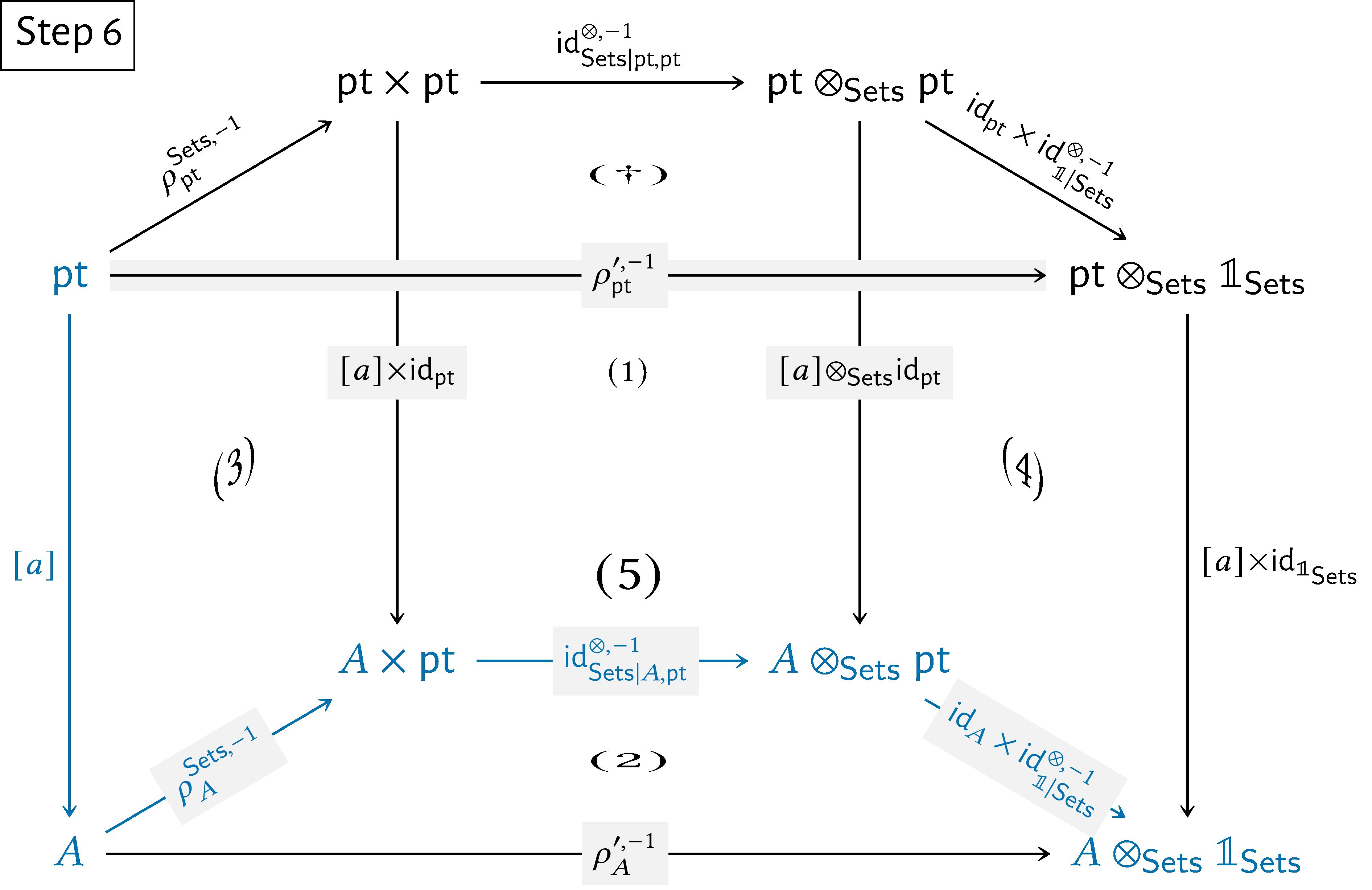
We then have
\begin{align*} \rho ^{\prime ,-1}_{A}\webleft (a\webright ) & = \webleft [\rho ^{\prime ,-1}_{A}\circ \webleft [a\webright ]\webright ]\webleft (\star \webright )\\ & = \webleft [\webleft (\operatorname {\mathrm{id}}_{A}\times \operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathbb {1}|\mathsf{Sets}}\webright )\circ \operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathsf{Sets}|\mathrm{pt},A}\circ \rho ^{\mathsf{Sets},-1}_{A}\circ \webleft [a\webright ]\webright ]\webleft (\star \webright )\\ & = \webleft [\webleft (\operatorname {\mathrm{id}}_{A}\times \operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathbb {1}|\mathsf{Sets}}\webright )\circ \operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathsf{Sets}|\mathrm{pt},A}\circ \rho ^{\mathsf{Sets},-1}_{A}\webright ]\webleft (a\webright ) \end{align*}
for each $a\in A$, and thus we have
\[ \rho ^{\prime ,-1}_{A}=\webleft (\operatorname {\mathrm{id}}_{A}\times \operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathbb {1}|\mathsf{Sets}}\webright )\circ \operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathsf{Sets}|\mathrm{pt},A}\circ \rho ^{\mathsf{Sets},-1}_{A}. \]
Taking inverses then gives
\[ \rho ^{\prime }_{A}=\rho ^{\mathsf{Sets}}_{A}\circ \operatorname {\mathrm{id}}^{\otimes }_{\mathsf{Sets}|\mathrm{pt},A}\circ \webleft (\operatorname {\mathrm{id}}_{A}\times \operatorname {\mathrm{id}}^{\otimes }_{\mathbb {1}|\mathsf{Sets}}\webright ), \]
showing that the diagram
indeed commutes.
Monoidality of the Isomorphism $\mathord {\otimes _{\mathsf{Sets}}}\cong \mathord {\times }$
We have to show that the diagram
commutes. First, note that the diagram
commutes by the terminality of $\mathrm{pt}$ (
Chapter 4: Constructions With Sets,
Construction 4.1.1.1.2). Since the map $!_{\mathrm{pt}\times \webleft (\mathrm{pt}\times \mathrm{pt}\webright )}\colon \mathrm{pt}\times \webleft (\mathrm{pt}\times \mathrm{pt}\webright )\to \mathrm{pt}$ is an isomorphism (e.g. having inverse $\lambda ^{\mathsf{Sets},-1}_{\mathrm{pt}}\circ \lambda ^{\mathsf{Sets},-1}_{\mathrm{pt}}$), it follows that the diagram
also commutes. Taking inverses, we see that the diagram
commutes as well. Now, let $A,B,C\in \operatorname {\mathrm{Obj}}\webleft (\mathsf{Sets}\webright )$, let $a\in A$, let $b\in B$, let $c\in C$, and consider the diagram
which we partition into subdiagrams as follows:
Since:
-
•
Subdiagram $\webleft (1\webright )$ commutes by the naturality of $\alpha ^{\mathsf{Sets},-1}$.
-
•
Subdiagram $\webleft (2\webright )$ commutes by the naturality of $\operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathsf{Sets}}$.
-
•
Subdiagram $\webleft (3\webright )$ commutes by the naturality of $\operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathsf{Sets}}$.
-
•
Subdiagram $\webleft (\dagger \webright )$ commutes, as proved above.
-
•
Subdiagram $\webleft (4\webright )$ commutes by the naturality of $\operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathsf{Sets}}$.
-
•
Subdiagram $\webleft (5\webright )$ commutes by the naturality of $\operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathsf{Sets}}$.
-
•
Subdiagram $\webleft (6\webright )$ commutes by the naturality of $\alpha ^{\prime ,-1}$.
it follows that the diagram
also commutes. We then have
\begin{align*} \left[\webleft (\operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathsf{Sets}|A,B}\otimes _{\mathsf{Sets}}\operatorname {\mathrm{id}}_{C}\webright )\circ \operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathsf{Sets}|A\times B,C}\right.\\ \left.{}\circ \alpha ^{\mathsf{Sets},-1}_{A,B,C}\right]\webleft (a,\webleft (b,c\webright )\webright ) & = \left[\webleft (\operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathsf{Sets}|A,B}\otimes _{\mathsf{Sets}}\operatorname {\mathrm{id}}_{C}\webright )\circ \operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathsf{Sets}|A\times B,C}\right.\\ & \phantom{={}} \mkern 4mu\left.{}{}\circ \alpha ^{\mathsf{Sets},-1}_{A,B,C}\circ \webleft (\webleft [a\webright ]\times \webleft (\webleft [b\webright ]\times \webleft [c\webright ]\webright )\webright )\right]\webleft (\star ,\webleft (\star ,\star \webright )\webright )\\ & = \left[\alpha ^{\prime ,-1}_{A,B,C}\circ \webleft (\operatorname {\mathrm{id}}_{A}\times \operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathsf{Sets}|B,C}\webright )\right.\\ & \phantom{={}} \mkern 4mu\left.{}\circ \operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathsf{Sets}|A,B\times C}\circ \webleft (\webleft [a\webright ]\times \webleft (\webleft [b\webright ]\times \webleft [c\webright ]\webright )\webright )\right]\webleft (\star ,\webleft (\star ,\star \webright )\webright )\\ & = \webleft [\alpha ^{\prime ,-1}_{A,B,C}\circ \webleft (\operatorname {\mathrm{id}}_{A}\times \operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathsf{Sets}|B,C}\webright )\circ \operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathsf{Sets}|A,B\times C}\webright ]\webleft (a,\webleft (b,c\webright )\webright ) \end{align*}
for each $\webleft (a,\webleft (b,c\webright )\webright )\in A\times \webleft (B\times C\webright )$, and thus we have Taking inverses then gives showing that the diagram
indeed commutes.
Braidedness of the Isomorphism $\mathord {\otimes _{\mathsf{Sets}}}\cong \mathord {\times }$
We have to show that the diagram
commutes. First, note that the diagram
commutes by the terminality of $\mathrm{pt}$ (
Chapter 4: Constructions With Sets,
Construction 4.1.1.1.2). Since the map $!_{\mathrm{pt}\times \mathrm{pt}}\colon \mathrm{pt}\times \mathrm{pt}\to \mathrm{pt}$ is invertible (e.g. with inverse $\lambda ^{\mathsf{Sets},-1}_{\mathrm{pt}}$), the diagram
also commutes. Taking inverses, we see that the diagram
commutes as well. Now, let $A,B\in \operatorname {\mathrm{Obj}}\webleft (\mathsf{Sets}\webright )$, let $a\in A$, let $b\in B$, and consider the diagram
which we partition into subdiagrams as follows:
Since:
-
•
Subdiagram $\webleft (2\webright )$ commutes by the naturality of $\sigma ^{\mathsf{Sets},-1}$.
-
•
Subdiagram $\webleft (5\webright )$ commutes by the naturality of $\operatorname {\mathrm{id}}^{\otimes ,-1}$.
-
•
Subdiagram $\webleft (\dagger \webright )$ commutes, as proved above.
-
•
Subdiagram $\webleft (4\webright )$ commutes by the naturality of $\sigma ^{\prime ,-1}$.
-
•
Subdiagram $\webleft (1\webright )$ commutes by the naturality of $\operatorname {\mathrm{id}}^{\otimes ,-1}$.
it follows that the diagram
commutes. We then have
\begin{align*} \webleft [\operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathsf{Sets}|A,B}\circ \sigma ^{\mathsf{Sets},-1}_{A,B}\webright ]\webleft (b,a\webright ) & = \webleft [\operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathsf{Sets}|A,B}\circ \sigma ^{\mathsf{Sets},-1}_{A,B}\circ \webleft (\webleft [b\webright ]\times \webleft [a\webright ]\webright )\webright ]\webleft (\star ,\star \webright )\\ & = \webleft [\sigma ^{\prime ,-1}_{A,B}\circ \operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathsf{Sets}|B,A}\circ \webleft (\webleft [b\webright ]\times \webleft [a\webright ]\webright )\webright ]\webleft (\star ,\star \webright )\\ & = \webleft [\sigma ^{\prime ,-1}_{A,B}\circ \operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathsf{Sets}|B,A}\webright ]\webleft (b,a\webright ) \end{align*}
for each $\webleft (b,a\webright )\in B\times A$, and thus we have
\[ \operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathsf{Sets}|A,B}\circ \sigma ^{\mathsf{Sets},-1}_{A,B}=\sigma ^{\prime ,-1}_{A,B}\circ \operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathsf{Sets}|B,A}. \]
Taking inverses then gives
\[ \sigma ^{\mathsf{Sets}}_{A,B}\circ \operatorname {\mathrm{id}}^{\otimes }_{\mathsf{Sets}|A,B}=\operatorname {\mathrm{id}}^{\otimes }_{\mathsf{Sets}|B,A}\circ \sigma ^{\prime }_{A,B}, \]
showing that the diagram
indeed commutes.
Uniqueness of the Isomorphism $\mathord {\otimes _{\mathsf{Sets}}}\cong \mathord {\times }$
Let $\phi ,\psi \colon -_{1}\otimes _{\mathsf{Sets}}-_{2}\Rightarrow -_{1}\times -_{2}$ be natural isomorphisms. Since these isomorphisms are compatible with the unitors of $\mathsf{Sets}$ with respect to $\times $ and $\otimes $ (as shown above), we have
\begin{align*} \lambda '_{B} & = \lambda ^{\mathsf{Sets}}_{B}\circ \phi _{\mathrm{pt},B}\circ \webleft (\operatorname {\mathrm{id}}^{\otimes }_{\mathbb {1}|\mathsf{Sets}}\otimes _{\mathsf{Sets}}\operatorname {\mathrm{id}}_{Y}\webright ),\\ \lambda '_{B} & = \lambda ^{\mathsf{Sets}}_{B}\circ \psi _{\mathrm{pt},B}\circ \webleft (\operatorname {\mathrm{id}}^{\otimes }_{\mathbb {1}|\mathsf{Sets}}\otimes _{\mathsf{Sets}}\operatorname {\mathrm{id}}_{Y}\webright ). \end{align*}
Postcomposing both sides with $\lambda ^{\mathsf{Sets},-1}_{B}$ gives
\begin{align*} \lambda ^{\mathsf{Sets},-1}_{B}\circ \lambda '_{B}\circ \webleft (\operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathbb {1}|\mathsf{Sets}}\otimes _{\mathsf{Sets}}\operatorname {\mathrm{id}}_{Y}\webright ) & = \phi _{\mathrm{pt},B},\\ \lambda ^{\mathsf{Sets},-1}_{B}\circ \lambda '_{B}\circ \webleft (\operatorname {\mathrm{id}}^{\otimes }_{\mathbb {1}|\mathsf{Sets}}\otimes _{\mathsf{Sets}}\operatorname {\mathrm{id}}_{Y}\webright ) & = \psi _{\mathrm{pt},B}, \end{align*}
and thus we have
\[ \phi _{\mathrm{pt},B}=\psi _{\mathrm{pt},B} \]
for each $B\in \operatorname {\mathrm{Obj}}\webleft (\mathsf{Sets}\webright )$. Now, let $a\in A$ and consider the naturality diagrams
for $\phi $ and $\psi $ with respect to the morphisms $\webleft [a\webright ]$ and $\operatorname {\mathrm{id}}_{B}$. Having shown that $\phi _{\mathrm{pt},B}=\psi _{\mathrm{pt},B}$, we have
\begin{align*} \phi _{A,B}\webleft (a,b\webright ) & = \webleft [\phi _{A,B}\circ \webleft (\webleft [a\webright ]\times \operatorname {\mathrm{id}}_{B}\webright )\webright ]\webleft (\star ,b\webright )\\ & = \webleft [\webleft (\webleft [a\webright ]\otimes _{\mathsf{Sets}}\operatorname {\mathrm{id}}_{B}\webright )\circ \phi _{\mathrm{pt},B}\webright ]\webleft (\star ,b\webright )\\ & = \webleft [\webleft (\webleft [a\webright ]\otimes _{\mathsf{Sets}}\operatorname {\mathrm{id}}_{B}\webright )\circ \psi _{\mathrm{pt},B}\webright ]\webleft (\star ,b\webright )\\ & = \webleft [\psi _{A,B}\circ \webleft (\webleft [a\webright ]\times \operatorname {\mathrm{id}}_{B}\webright )\webright ]\webleft (\star ,b\webright )\\ & = \psi _{A,B}\webleft (a,b\webright ) \end{align*}
for each $\webleft (a,b\webright )\in A\times B$. Therefore we have
\[ \phi _{A,B}=\psi _{A,B} \]
for each $A,B\in \operatorname {\mathrm{Obj}}\webleft (\mathsf{Sets}\webright )$ and thus $\phi =\psi $, showing the isomorphism $\mathord {\otimes _{\mathsf{Sets}}}\cong \mathord {\times }$ to be unique.
The symmetric monoidal structure on the category $\mathsf{Sets}$ of Proposition 5.1.9.1.1 is uniquely determined by the following requirements:
-
1.
Two-Sided Preservation of Colimits. The tensor product
\[ \otimes _{\mathsf{Sets}}\colon \mathsf{Sets}\times \mathsf{Sets}\to \mathsf{Sets} \]
of $\mathsf{Sets}$ preserves colimits separately in each variable.
-
2.
The Unit Object Is $\mathrm{pt}$. We have $\mathbb {1}_{\mathsf{Sets}}\cong \mathrm{pt}$.
More precisely, the full subcategory of the category $\mathcal{M}_{\mathbb {E}_{\infty }}\webleft (\mathsf{Sets}\webright )$ of spanned by the symmetric monoidal categories $\webleft (\mathsf{Sets},\otimes _{\mathsf{Sets}},\mathbb {1}_{\mathsf{Sets}},\lambda ^{\mathsf{Sets}},\rho ^{\mathsf{Sets}},\sigma ^{\mathsf{Sets}}\webright )$ satisfying Item 1 and Item 2 is contractible.
Since $\mathsf{Sets}$ is locally presentable (), it follows from that Item 1 is equivalent to the existence of an internal Hom as in Item 1 of Theorem 5.1.10.1.1. The result then follows from Theorem 5.1.10.1.1.
