The Clowder Project

5.1.10 The Universal Property of $(\mathsf{Sets},\times ,\mathrm{pt})$

The symmetric monoidal structure on the category $\mathsf{Sets}$ of Proposition 5.1.9.1.1 is uniquely determined by the following requirements:

1. 1.

   Existence of an Internal Hom. The tensor product

   \[ \otimes _{\mathsf{Sets}}\colon \mathsf{Sets}\times \mathsf{Sets}\to \mathsf{Sets} \]

   of $\mathsf{Sets}$ admits an internal Hom $[-_{1},-_{2}]_{\mathsf{Sets}}$.

2. 2.

   The Unit Object Is $\mathrm{pt}$. We have $\mathbb {1}_{\mathsf{Sets}}\cong \mathrm{pt}$.

More precisely, the full subcategory of the category $\mathcal{M}^{\mathrm{cld}}_{\mathbb {E}_{\infty }}(\mathsf{Sets})$ of spanned by the closed symmetric monoidal categories $\left(\phantom{\mathrlap {\lambda ^{\mathsf{Sets}}}}\mathsf{Sets}\right.$, $\otimes _{\mathsf{Sets}}$, $[-_{1},-_{2}]_{\mathsf{Sets}}$, $\mathbb {1}_{\mathsf{Sets}}$, $\lambda ^{\mathsf{Sets}}$, $\rho ^{\mathsf{Sets}}$, $\left.\sigma ^{\mathsf{Sets}}\right)$ satisfying Item 1 and Item 2 is contractible (i.e. equivalent to the punctual category).

Unwinding the Statement

Let $(\mathsf{Sets},\otimes _{\mathsf{Sets}},[-_{1},-_{2}]_{\mathsf{Sets}},\mathbb {1}_{\mathsf{Sets}},\lambda ',\rho ',\sigma ')$ be a closed symmetric monoidal category satisfying Item 1 and Item 2. We need to show that the identity functor

\[ \operatorname {\mathrm{id}}_{\mathsf{Sets}}\colon \mathsf{Sets}\to \mathsf{Sets} \]

admits a unique closed symmetric monoidal functor structure

\[ \begin{array}{cccc} \phantom{\operatorname {\mathrm{id}}^{\otimes }_{\mathsf{Sets}}}\mathllap {\operatorname {\mathrm{id}}^{\otimes }_{\mathsf{Sets}}} \colon \mkern -10mu & A\otimes _{\mathsf{Sets}}B \mkern -10mu& {}\mathbin {\overset {\scriptstyle \mathord {\sim }}{\dashrightarrow }}& \mkern -10mu{}A\times B,\\ \phantom{\operatorname {\mathrm{id}}^{\otimes }_{\mathsf{Sets}}}\mathllap {\operatorname {\mathrm{id}}^{\operatorname {\mathrm{Hom}}}_{\mathsf{Sets}}} \colon \mkern -10mu & [A,B]_{\mathsf{Sets}} \mkern -10mu& {}\mathbin {\overset {\scriptstyle \mathord {\sim }}{\dashrightarrow }}& \mkern -10mu{}\mathsf{Sets}(A,B),\\ \phantom{\operatorname {\mathrm{id}}^{\otimes }_{\mathsf{Sets}}}\mathllap {\operatorname {\mathrm{id}}^{\otimes }_{\mathbb {1}|\mathsf{Sets}}} \colon \mkern -10mu & \mathbb {1}_{\mathsf{Sets}} \mkern -10mu& {}\mathbin {\overset {\scriptstyle \mathord {\sim }}{\dashrightarrow }}& \mkern -10mu{}\mathrm{pt}, \end{array} \]

making it into a symmetric monoidal strongly closed isomorphism of categories from $\left(\phantom{\mathrlap {\lambda '}}\mathsf{Sets}\right.$, $\otimes _{\mathsf{Sets}}$, $[-_{1},-_{2}]_{\mathsf{Sets}}$, $\mathbb {1}_{\mathsf{Sets}}$, $\lambda '$, $\rho '$, $\left.\sigma '\right)$ to the closed symmetric monoidal category $\left(\phantom{\mathrlap {\lambda ^{\mathsf{Sets}}}}\mathsf{Sets}\right.$, $\times $, $\mathsf{Sets}(-_{1},-_{2})$, $\mathbb {1}_{\mathsf{Sets}}$, $\lambda ^{\mathsf{Sets}}$, $\rho ^{\mathsf{Sets}}$, $\left.\sigma ^{\mathsf{Sets}}\right)$ of Proposition 5.1.9.1.1.

Constructing an Isomorphism $[-_{1},-_{2}]_{\mathsf{Sets}}\cong \mathsf{Sets}(-_{1},-_{2})$

By , we have a natural isomorphism

\[ \mathsf{Sets}(\mathrm{pt},[-_{1},-_{2}]_{\mathsf{Sets}})\cong \mathsf{Sets}(-_{1},-_{2}). \]

By Chapter 4: Constructions With Sets, Item 3 of Proposition 4.3.5.1.2, we also have a natural isomorphism

\[ \mathsf{Sets}(\mathrm{pt},[-_{1},-_{2}]_{\mathsf{Sets}})\cong [-_{1},-_{2}]_{\mathsf{Sets}}. \]

Composing both natural isomorphisms, we obtain a natural isomorphism

\[ \mathsf{Sets}(-_{1},-_{2})\cong [-_{1},-_{2}]_{\mathsf{Sets}}. \]

Given $A,B\in \operatorname {\mathrm{Obj}}(\mathsf{Sets})$, we will write

\[ \operatorname {\mathrm{id}}^{\operatorname {\mathrm{Hom}}}_{A,B}\colon \mathsf{Sets}(A,B)\overset {\scriptstyle \mathord {\sim }}{\dashrightarrow }[A,B]_{\mathsf{Sets}} \]

for the component of this isomorphism at $(A,B)$.

Constructing an Isomorphism $\mathord {\otimes _{\mathsf{Sets}}}\cong \mathord {\times }$

Since $\otimes _{\mathsf{Sets}}$ is adjoint in each variable to $[-_{1},-_{2}]_{\mathsf{Sets}}$ by assumption and $\times $ is adjoint in each variable to $\mathsf{Sets}(-_{1},-_{2})$ by Chapter 4: Constructions With Sets, Item 2 of Proposition 4.3.5.1.2, uniqueness of adjoints () gives us natural isomorphisms

\begin{align*} A\otimes _{\mathsf{Sets}}- & \cong A\times -,\\ -\otimes _{\mathsf{Sets}}B & \cong B\times -. \end{align*}

By , we then have $\mathord {\otimes _{\mathsf{Sets}}}\cong \mathord {\times }$. We will write

\[ \operatorname {\mathrm{id}}^{\otimes }_{\mathsf{Sets}|A,B}\colon A\otimes _{\mathsf{Sets}}B\overset {\scriptstyle \mathord {\sim }}{\dashrightarrow }A\times B \]

for the component of this isomorphism at $(A,B)$.

Alternative Construction of an Isomorphism $\mathord {\otimes _{\mathsf{Sets}}}\cong \mathord {\times }$

Alternatively, we may construct a natural isomorphism $\mathord {\otimes _{\mathsf{Sets}}}\cong \mathord {\times }$ as follows:

1. 1.

   Let $A\in \operatorname {\mathrm{Obj}}(\mathsf{Sets})$.

2. 2.

   Since $\otimes _{\mathsf{Sets}}$ is part of a closed monoidal structure, it preserves colimits in each variable by .

3. 3.

   Since $A\cong \mathchoice {\mathbin {\textstyle \coprod }}{\mathbin {\textstyle \coprod }}{\mathbin {\scriptstyle \textstyle \coprod }}{\mathbin {\scriptscriptstyle \textstyle \coprod }}_{a\in A}\mathrm{pt}$ and $\otimes _{\mathsf{Sets}}$ preserves colimits in each variable, we have

   \begin{align*} A\otimes _{\mathsf{Sets}}B & \cong (\coprod _{a\in A}\mathrm{pt})\otimes _{\mathsf{Sets}}B\\ & \cong \coprod _{a\in A}(\mathrm{pt}\otimes _{\mathsf{Sets}}B)\\ & \cong \coprod _{a\in A}B\\ & \cong A\times B, \end{align*}

   naturally in $B\in \operatorname {\mathrm{Obj}}(\mathsf{Sets})$, where we have used that $\mathrm{pt}$ is the monoidal unit for $\otimes _{\mathsf{Sets}}$. Thus $A\otimes _{\mathsf{Sets}}-\cong A\times -$ for each $A\in \operatorname {\mathrm{Obj}}(\mathsf{Sets})$.

5.

By , we then have $\mathord {\otimes _{\mathsf{Sets}}}\cong \mathord {\times }$.

Below, we’ll show that if a natural isomorphism $\mathord {\otimes _{\mathsf{Sets}}}\cong \mathord {\times }$ exists, then it must be unique. This will show that the isomorphism constructed above is equal to the isomorphism $\operatorname {\mathrm{id}}^{\otimes }_{\mathsf{Sets}|A,B}\colon A\otimes _{\mathsf{Sets}}B\to A\times B$ from before.

We define an isomorphism $\operatorname {\mathrm{id}}^{\otimes }_{\mathbb {1}}\colon \mathbb {1}_{\mathsf{Sets}}\to \mathrm{pt}$ as the composition

in $\mathsf{Sets}$.

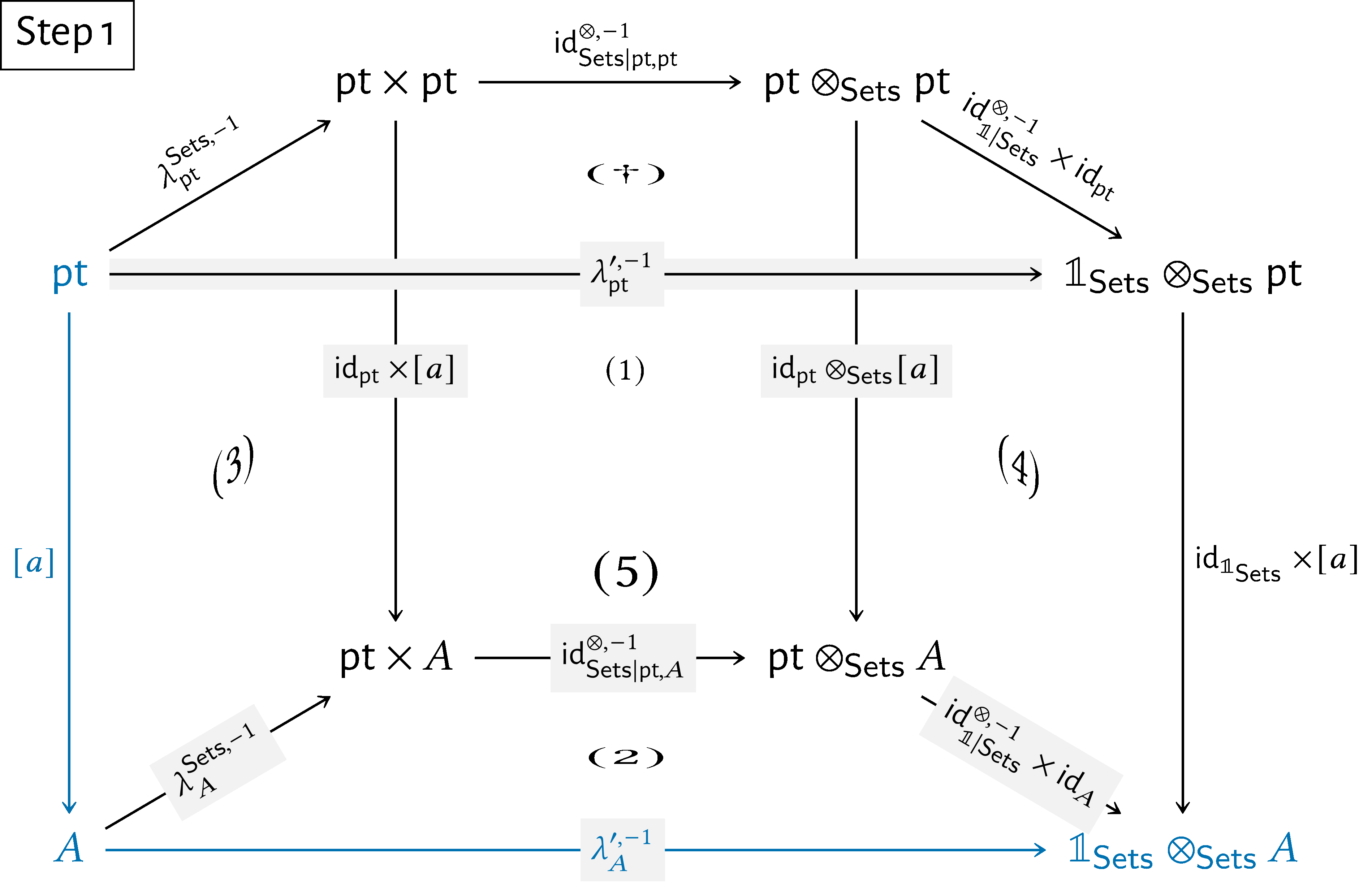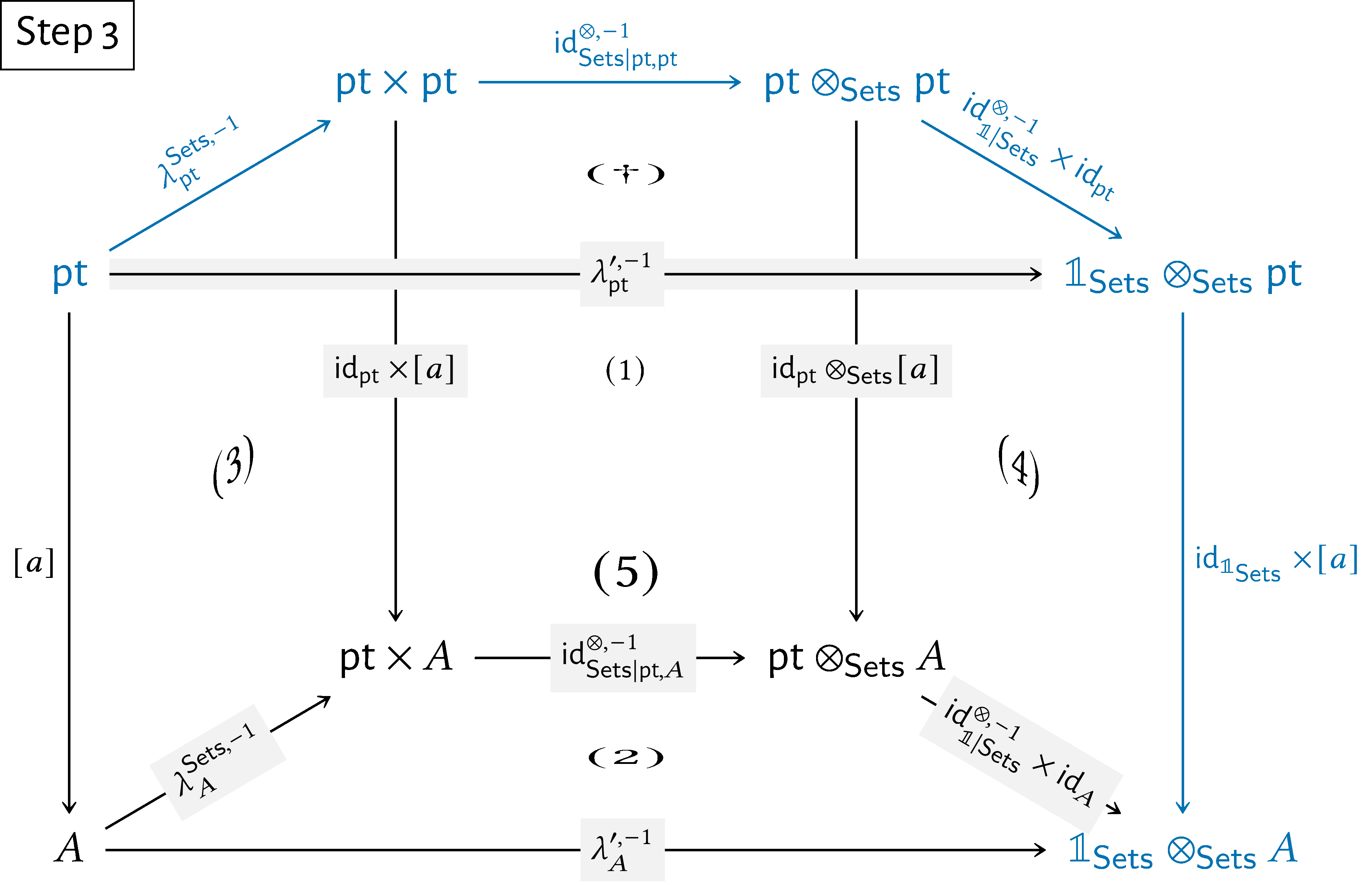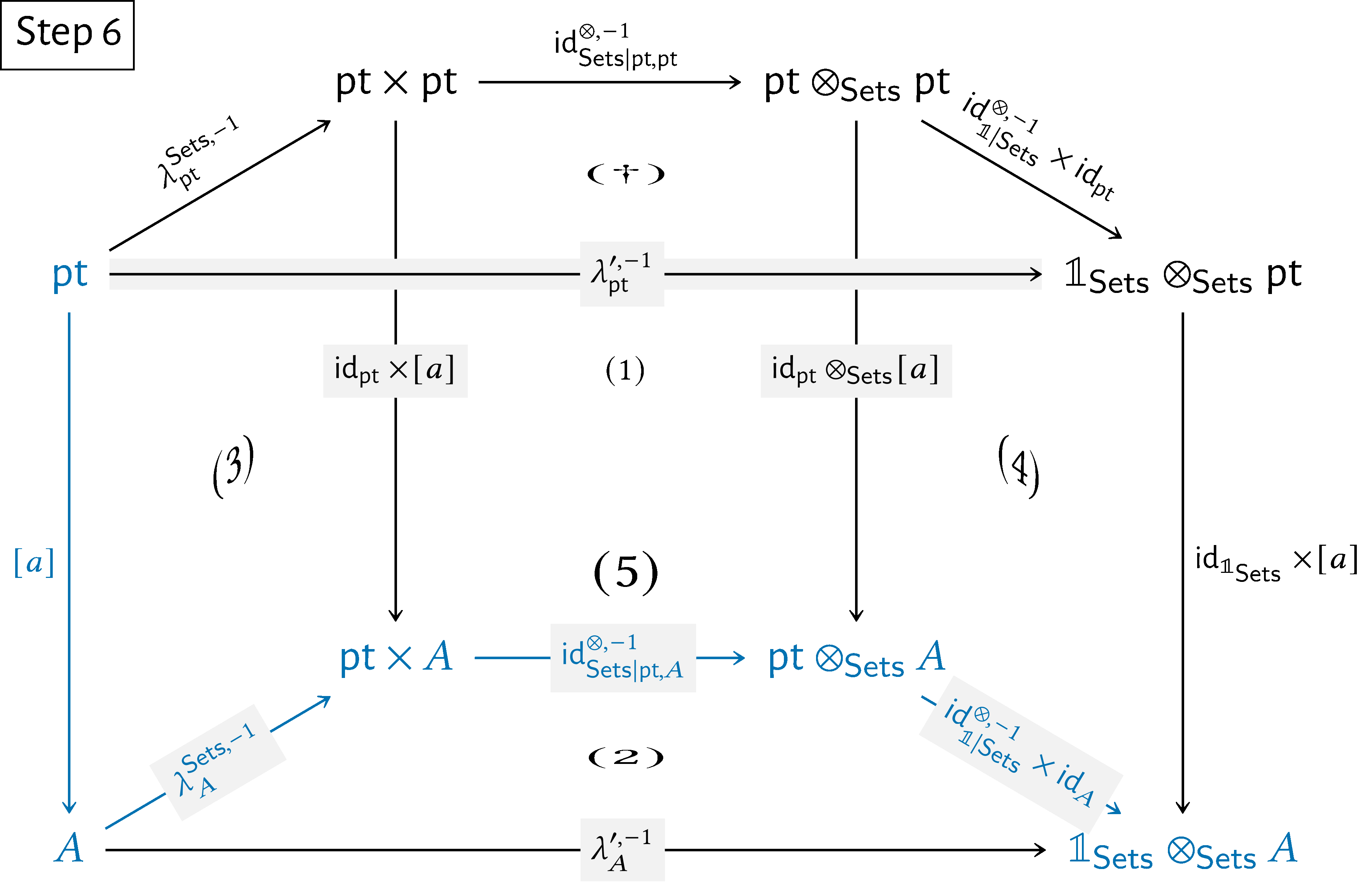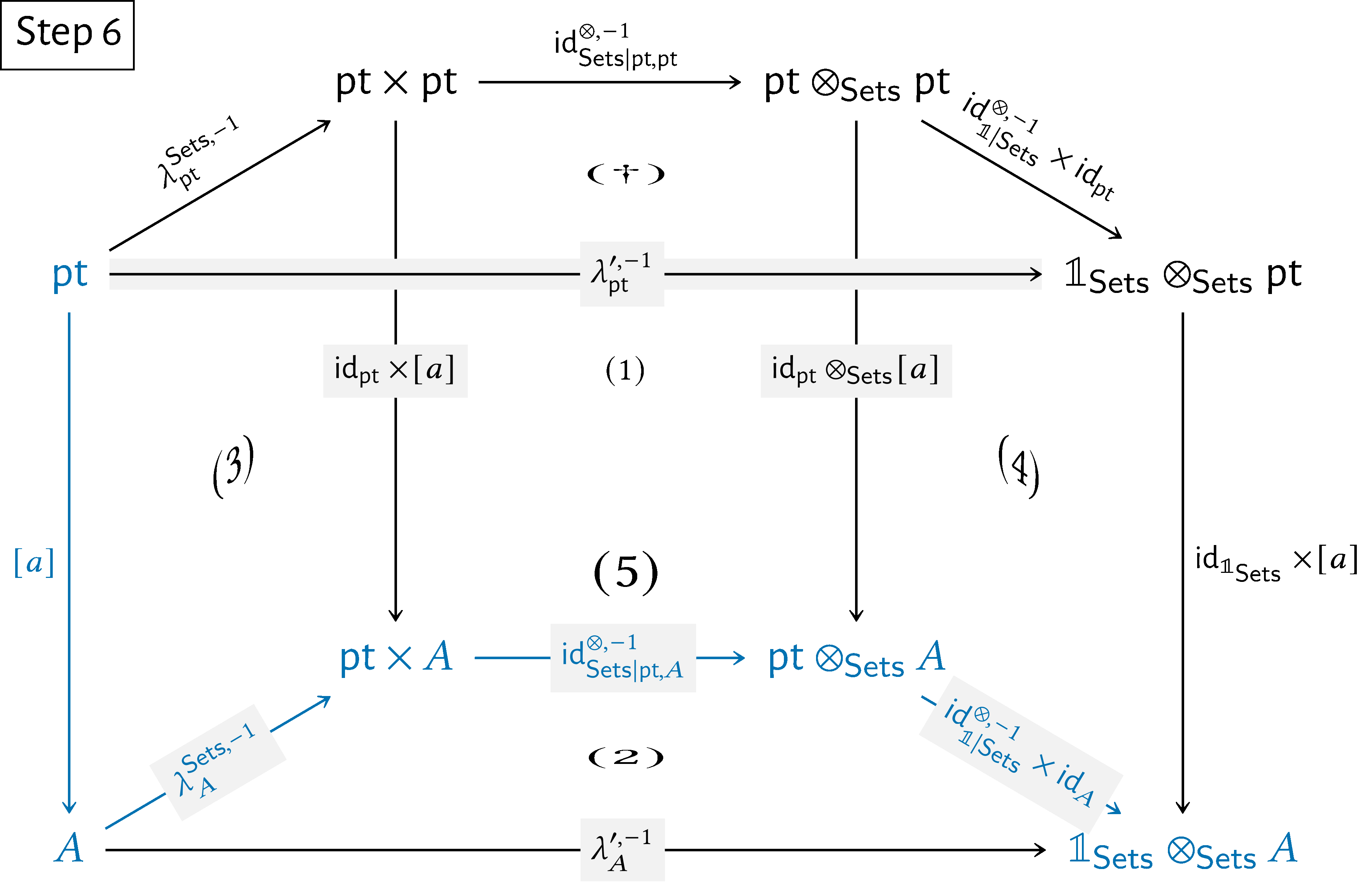
We have to show that the diagram commutes. First, note that the diagram corresponding to the case $A=\mathrm{pt}$, commutes by the terminality of $\mathrm{pt}$ (Chapter 4: Constructions With Sets, Construction 4.1.1.1.2). Since this diagram commutes, so does the diagram Now, let $A\in \operatorname {\mathrm{Obj}}(\mathsf{Sets})$, let $a\in A$, and consider the diagram Since:

• •

  Subdiagram $(5)$ commutes by the naturality of $\lambda ^{\prime ,-1}$.

• •

  Subdiagram $(\dagger )$ commutes, as proved above.

• •

  Subdiagram $(4)$ commutes by the naturality of $\operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathbb {1}|\mathsf{Sets}}$.

• •

  Subdiagram $(1)$ commutes by the naturality of $\operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathsf{Sets}}$.

• •

  Subdiagram $(3)$ commutes by the naturality of $\lambda ^{\mathsf{Sets},-1}$.

it follows that the diagram

We then have

for each $a\in A$, and thus we have

Taking inverses then gives

showing that the diagram

indeed commutes.

We can use the same argument we used to prove the monoidal left unity of the isomorphism $\mathord {\otimes _{\mathsf{Sets}}}\cong \mathord {\times }$ above. For completeness, we repeat it below.

We have to show that the diagram

commutes. First, note that the diagram corresponding to the case $A=\mathrm{pt}$, commutes by the terminality of $\mathrm{pt}$ (Chapter 4: Constructions With Sets, Construction 4.1.1.1.2). Since this diagram commutes, so does the diagram Now, let $A\in \operatorname {\mathrm{Obj}}(\mathsf{Sets})$, let $a\in A$, and consider the diagram Since:

• •

  Subdiagram $(5)$ commutes by the naturality of $\rho ^{\prime ,-1}$.

• •

  Subdiagram $(\dagger )$ commutes, as proved above.

• •

  Subdiagram $(4)$ commutes by the naturality of $\operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathbb {1}|\mathsf{Sets}}$.

• •

  Subdiagram $(1)$ commutes by the naturality of $\operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathsf{Sets}}$.

• •

  Subdiagram $(3)$ commutes by the naturality of $\rho ^{\mathsf{Sets},-1}$.

it follows that the diagram

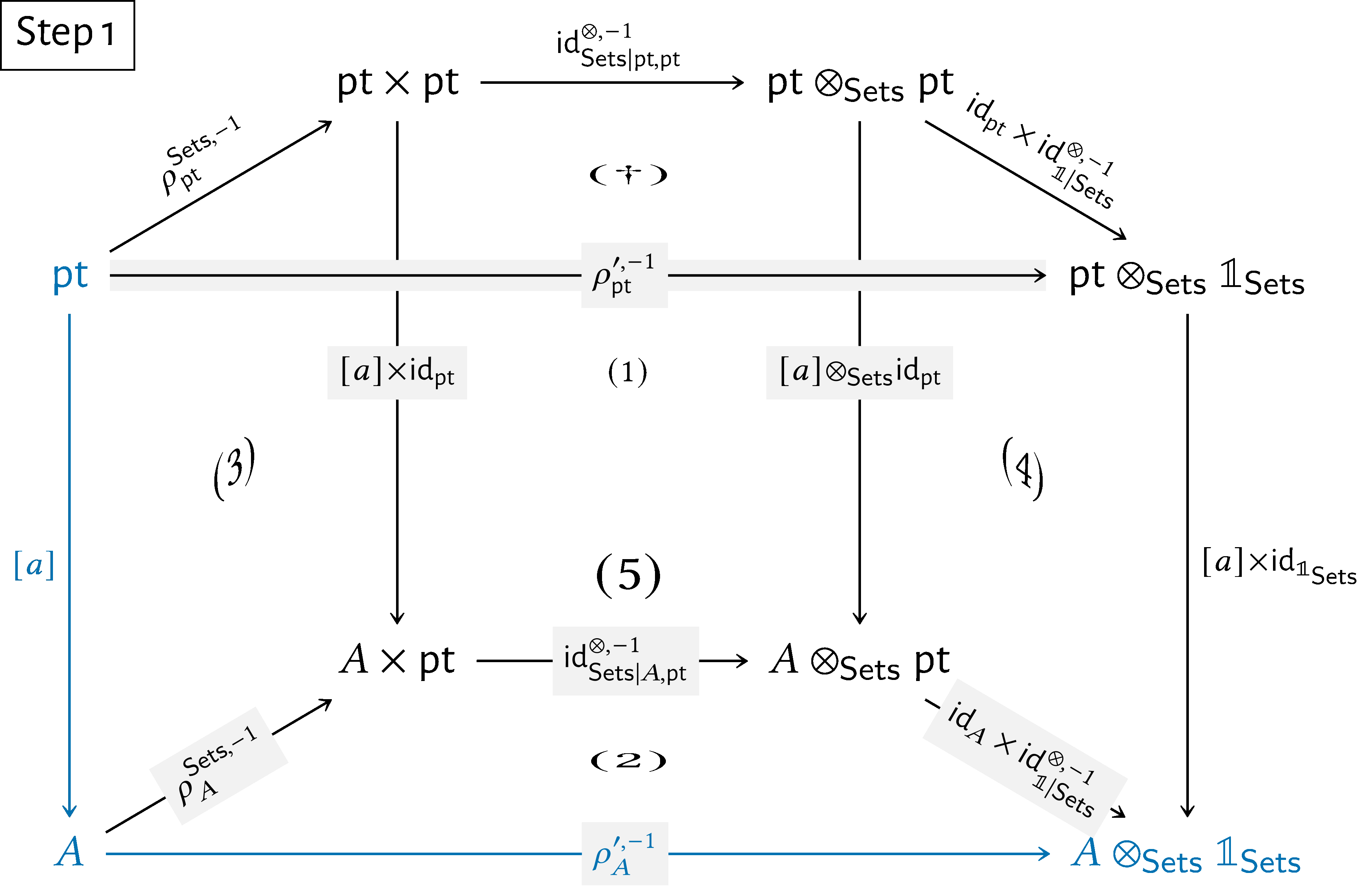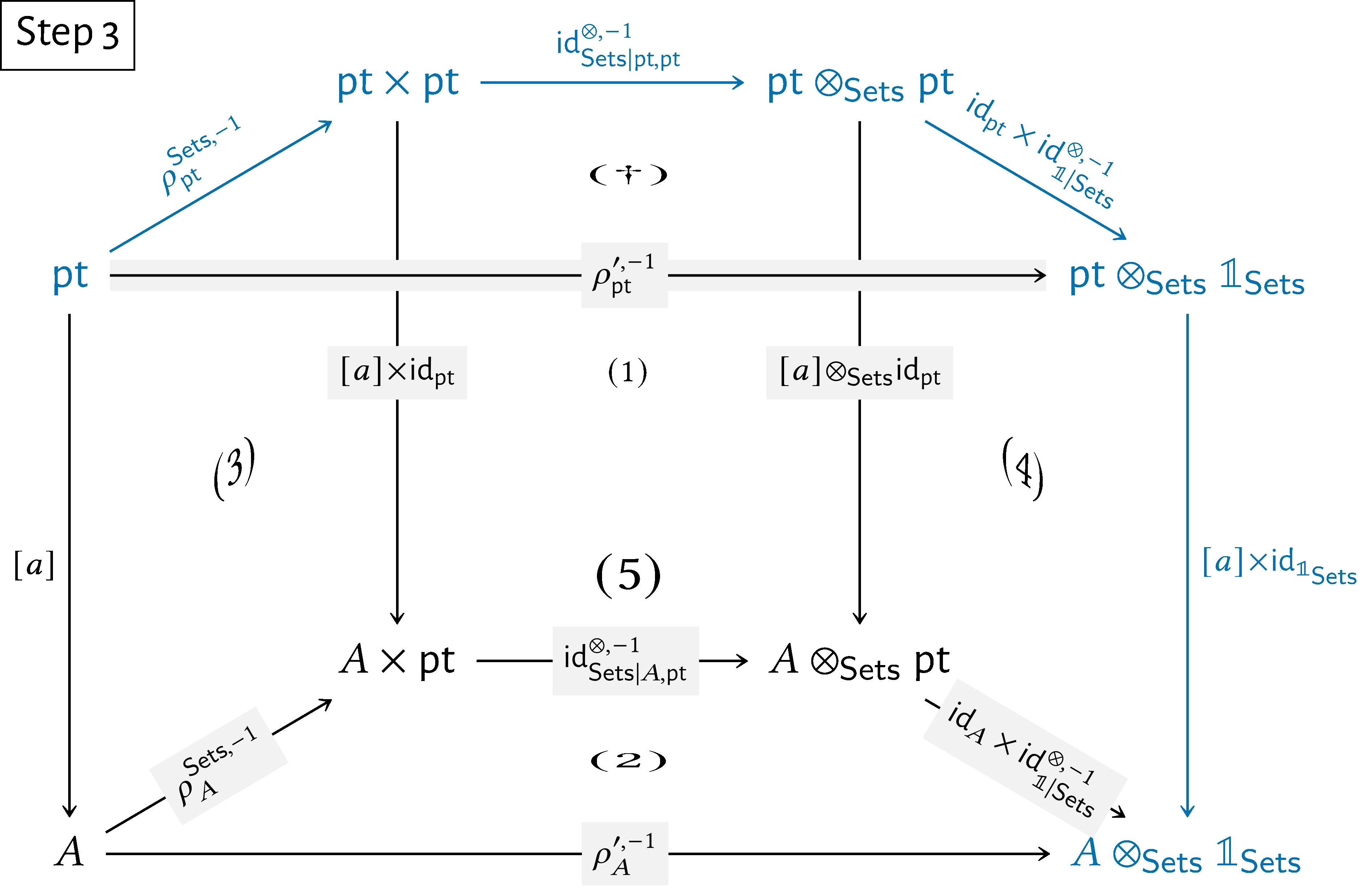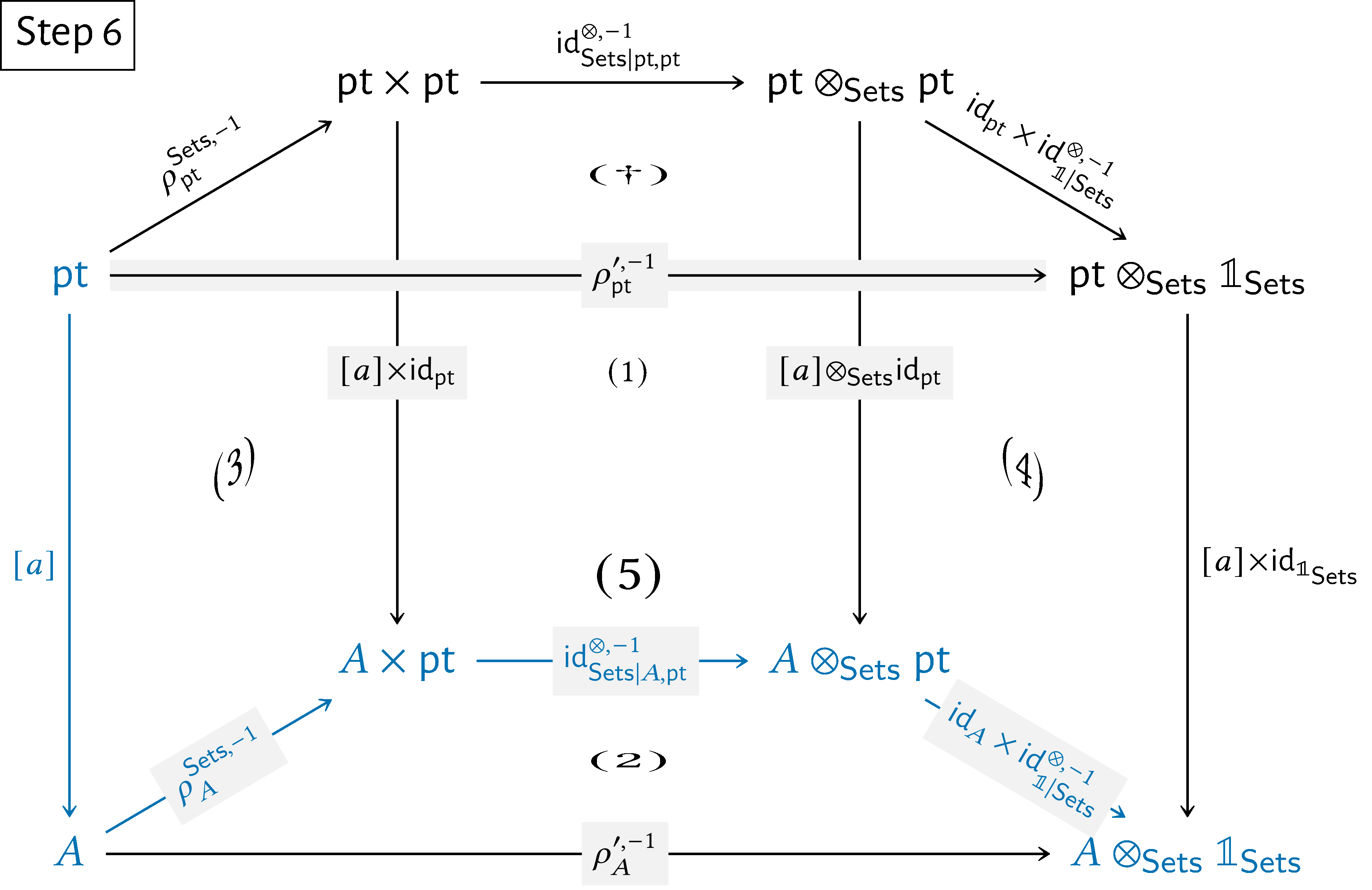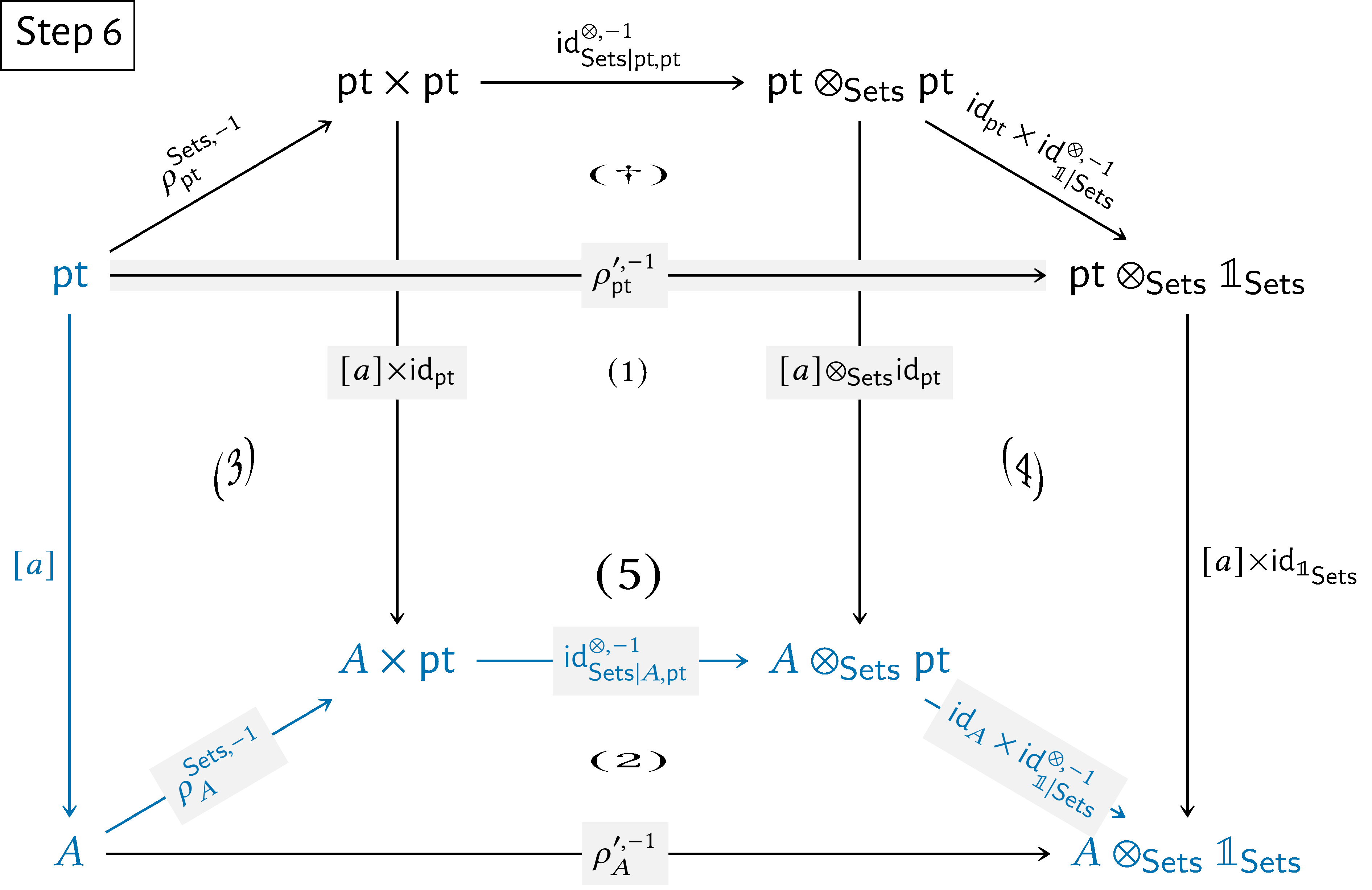
We then have

for each $a\in A$, and thus we have

Taking inverses then gives

showing that the diagram

indeed commutes.

We have to show that the diagram commutes. First, note that the diagram commutes by the terminality of $\mathrm{pt}$ (Chapter 4: Constructions With Sets, Construction 4.1.1.1.2). Since the map $!_{\mathrm{pt}\times (\mathrm{pt}\times \mathrm{pt})}\colon \mathrm{pt}\times (\mathrm{pt}\times \mathrm{pt})\to \mathrm{pt}$ is an isomorphism (e.g. having inverse $\lambda ^{\mathsf{Sets},-1}_{\mathrm{pt}}\circ \lambda ^{\mathsf{Sets},-1}_{\mathrm{pt}}$), it follows that the diagram also commutes. Taking inverses, we see that the diagram commutes as well. Now, let $A,B,C\in \operatorname {\mathrm{Obj}}(\mathsf{Sets})$, let $a\in A$, let $b\in B$, let $c\in C$, and consider the diagram which we partition into subdiagrams as follows: Since:

• •

  Subdiagram $(1)$ commutes by the naturality of $\alpha ^{\mathsf{Sets},-1}$.

• •

  Subdiagram $(2)$ commutes by the naturality of $\operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathsf{Sets}}$.

• •

  Subdiagram $(3)$ commutes by the naturality of $\operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathsf{Sets}}$.

• •

  Subdiagram $(\dagger )$ commutes, as proved above.

• •

  Subdiagram $(4)$ commutes by the naturality of $\operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathsf{Sets}}$.

• •

  Subdiagram $(5)$ commutes by the naturality of $\operatorname {\mathrm{id}}^{\otimes ,-1}_{\mathsf{Sets}}$.

• •

  Subdiagram $(6)$ commutes by the naturality of $\alpha ^{\prime ,-1}$.

it follows that the diagram

also commutes. We then have for each $(a,(b,c))\in A\times (B\times C)$, and thus we have Taking inverses then gives showing that the diagram indeed commutes.

We have to show that the diagram commutes. First, note that the diagram commutes by the terminality of $\mathrm{pt}$ (Chapter 4: Constructions With Sets, Construction 4.1.1.1.2). Since the map $!_{\mathrm{pt}\times \mathrm{pt}}\colon \mathrm{pt}\times \mathrm{pt}\to \mathrm{pt}$ is invertible (e.g. with inverse $\lambda ^{\mathsf{Sets},-1}_{\mathrm{pt}}$), the diagram also commutes. Taking inverses, we see that the diagram commutes as well. Now, let $A,B\in \operatorname {\mathrm{Obj}}(\mathsf{Sets})$, let $a\in A$, let $b\in B$, and consider the diagram which we partition into subdiagrams as follows: Since:

• •

  Subdiagram $(2)$ commutes by the naturality of $\sigma ^{\mathsf{Sets},-1}$.

• •

  Subdiagram $(5)$ commutes by the naturality of $\operatorname {\mathrm{id}}^{\otimes ,-1}$.

• •

  Subdiagram $(\dagger )$ commutes, as proved above.

• •

  Subdiagram $(4)$ commutes by the naturality of $\sigma ^{\prime ,-1}$.

• •

  Subdiagram $(1)$ commutes by the naturality of $\operatorname {\mathrm{id}}^{\otimes ,-1}$.

it follows that the diagram

commutes. We then have

for each $(b,a)\in B\times A$, and thus we have

Taking inverses then gives

showing that the diagram

indeed commutes.

Let $\phi ,\psi \colon -_{1}\otimes _{\mathsf{Sets}}-_{2}\Rightarrow -_{1}\times -_{2}$ be natural isomorphisms. Since these isomorphisms are compatible with the unitors of $\mathsf{Sets}$ with respect to $\times $ and $\otimes $ (as shown above), we have

Postcomposing both sides with $\lambda ^{\mathsf{Sets},-1}_{B}$ gives

and thus we have

for each $B\in \operatorname {\mathrm{Obj}}(\mathsf{Sets})$. Now, let $a\in A$ and consider the naturality diagrams

for $\phi $ and $\psi $ with respect to the morphisms $[a]$ and $\operatorname {\mathrm{id}}_{B}$. Having shown that $\phi _{\mathrm{pt},B}=\psi _{\mathrm{pt},B}$, we have

for each $(a,b)\in A\times B$. Therefore we have

for each $A,B\in \operatorname {\mathrm{Obj}}(\mathsf{Sets})$ and thus $\phi =\psi $, showing the isomorphism $\mathord {\otimes _{\mathsf{Sets}}}\cong \mathord {\times }$ to be unique.

The symmetric monoidal structure on the category $\mathsf{Sets}$ of Proposition 5.1.9.1.1 is uniquely determined by the following requirements:

1. 1.

   Two-Sided Preservation of Colimits. The tensor product

   \[ \otimes _{\mathsf{Sets}}\colon \mathsf{Sets}\times \mathsf{Sets}\to \mathsf{Sets} \]

   of $\mathsf{Sets}$ preserves colimits separately in each variable.

2. 2.

   The Unit Object Is $\mathrm{pt}$. We have $\mathbb {1}_{\mathsf{Sets}}\cong \mathrm{pt}$.

More precisely, the full subcategory of the category $\mathcal{M}_{\mathbb {E}_{\infty }}(\mathsf{Sets})$ of spanned by the symmetric monoidal categories $(\mathsf{Sets},\otimes _{\mathsf{Sets}},\mathbb {1}_{\mathsf{Sets}},\lambda ^{\mathsf{Sets}},\rho ^{\mathsf{Sets}},\sigma ^{\mathsf{Sets}})$ satisfying Item 1 and Item 2 is contractible.

Since $\mathsf{Sets}$ is locally presentable (), it follows from that Item 1 is equivalent to the existence of an internal Hom as in Item 1 of Theorem 5.1.10.1.1. The result then follows from Theorem 5.1.10.1.1.